15-puzzle – neverendingbooks

censured post : bloggers’ block

Published February 6, 2008 by lievenlb

Below an up-till-now hidden post, written november last year, trying to explain the long blog-silence at neverendingbooks during october-november 2007…

A couple of months ago a publisher approached me, out of the blue, to consider writing a book about mathematics for the general audience (in Dutch (?!)). Okay, I brought this on myself hinting at the possibility in this post

Recently, I’ve been playing with the idea of writing a book for the general public. Its title is still unclear to me (though an idea might be “The disposable science”, better suggestions are of course wellcome) but I’ve fixed the subtitle as “Mathematics’ puzzling fall from grace”. The book’s concept is simple : I would consider the mathematical puzzles creating an hype over the last three centuries : the 14-15 puzzle for the 19th century, Rubik’s cube for the 20th century and, of course, Sudoku for the present century.

For each puzzle, I would describe its origin, the mathematics involved and how it can be used to solve the puzzle and, finally, what the differing quality of these puzzles tells us about mathematics’ changing standing in society over the period. Needless to say, the subtitle already gives away my point of view. The final part of the book would then be more optimistic. What kind of puzzles should we promote for mathematical thinking to have a fighting chance to survive in the near future?

While I still like the idea and am considering the proposal, chances are low this book ever materializes : the blog-title says it all…

Then, about a month ago I got some incoming links from a variety of Flemish blogs. From their posts I learned that the leading Science-magazine for the low countries, Natuur, Wetenschap & Techniek (Nature, Science & Technology), featured an article on Flemish science-blogs and that this blog might be among the ones covered. It sure would explain the publisher’s sudden interest. Of course, by that time the relevant volume of NW&T was out of circulation so I had to order a backcopy to find out what was going on. Here’s the relevant section, written by their editor Erick Vermeulen (as well as an attempt to translate it)

Sliding puzzle For those who want more scientific depth (( their interpretation, not mine )), there is the English blog by Antwerp professor algebra & geometry Lieven Le Bruyn, MoonshineMath (( indicates when the article was written… )). Le Bruyn offers a number of mathematical descriptions, most of them relating to group theory and in particular the so called monster-group and monstrous moonshine. He mentions some puzzles in passing such as the well known sliding puzzle with 15 pieces sliding horizontally and vertically in a 4 by 4 matrix. Le Bruyn argues that this ’15-puzzle (( The 15-puzzle groupoid ))’ was the hype of the 19th century as was the Rubik cube for the 20th and is Sudoku for the 21st century.
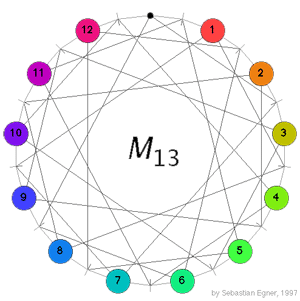
Interesting is Le Bruyn’s mathematical description of the M(13)-puzzle (( Conway’s M(13)-puzzle )) developed by John Conway. It has 13 points on a circle, twelve of them carrying a numbered counter. Every point is connected via lines to all others (( a slight simplification )). Whenever a counter jumps to the empty spot, two others exchange places. Le Bruyn promises the blog-visitor new variants to come (( did I? )). We are curious.
Of course, the genuine puzzler can leave all this theory for what it is, use the Java-applet (( Egner’s M(13)-applet )) and painfully try to move the counters around the circle according to the rules of the game.

Some people crave for this kind of media-attention. On me it merely has a blocking-effect. Still, as the end of my first-semester courses comes within sight, I might try to shake it off…

The Mathieu groupoid (1)

Published June 20, 2007 by lievenlb

Conway’s puzzle M(13) is a variation on the 15-puzzle played with the 13 points in the projective plane $\mathbb{P}^2(\mathbb{F}_3) $. The desired position is given on the left where all the counters are placed at at the points having that label (the point corresponding to the hole in the drawing has label 0). A typical move consists in choosing a line in the plane going through the point where the hole is, choose one of the three remaining points on this line and interchange the counter on it for the hole while at the same time interchanging the counters on the other two points. In the drawing on the left, lines correspond to the little-strokes on the circle and edges describe which points lie on which lines. For example, if we want to move counter 5 to the hole we notice that both of them lie on the line represented by the stroke just to the right of the hole and this line contains also the two points with counters 1 and 11, so we have to replace these two counters too in making a move. Today we will describe the groupoid corresponding to this slide-puzzle so if you want to read on, it is best to play a bit with Sebastian Egner’s M(13) Java Applet to see the puzzle in action (and to use it to verify the claims made below). Clicking on a counter performs the move taking the counter to the hole.

2 Comments

The 15-puzzle groupoid (2)

Published June 19, 2007 by lievenlb

In the 15-puzzle groupoid 1 we have seen that the legal positions of the classical 15-puzzle are the objects of a category in which every morphism is an isomorphism (a groupoid ). Today, we will show that there are exactly 10461394944000 objects (legal positions) in this groupoid. The crucial fact is that positions with the hole in a fixed place can be identified with the elements of the alternating group $A_{15} $, a fact first proved by William Edward Story in 1879 in a note published in the American Journal of Mathematics.

Recall from last time that the positions reachable from the initial position can be encoded as $\boxed{\tau} $ where $\tau $ is the permutation on 16 elements (the 15 numbered squares and 16 for the hole) such that $\tau(i) $ tells what number in the position lies on square $i $ of the initial position. The set of all reachable positions are the objects of our category. A morphism $\boxed{\tau} \rightarrow \boxed{\sigma} $ is a legal sequence of slide-moves starting from position $\boxed{\tau} $ and ending at position $\boxed{\sigma} $. That is,

$\boxed{\sigma} = (16,i_k)(16,i_{k-1}) \cdots (16,i_2)(16,i_1) \boxed{\tau} $

Tag: 15-puzzle

censured post : bloggers’ block

The Mathieu groupoid (1)

The 15-puzzle groupoid (2)