For what it is worth, Ive computed some more terms in the iguanodon series. Here they are
$L_2(7),M_{12},A_{16},M_{24},A_{28},A_{40},A_{48},A_{60},A_{68},A_{88},A_{96},A_{120},A_{132},A_{148},A_{164},A_{196},\ldots $
By construction, the n-th iguanodon group $Ig_n $ (corresponding to the n-th Farey sequence) is a subgroup of the alternating group on its (half)legs. Hence to prove that all remaining iguanodons are alternating groups boils down to proving that they are sufficiently transitive, for example, by showing that there are permutations of certain cycle-types in the group. Im sure any grouptheorist can crack this problem over lunch, so if you did please drop a comment.
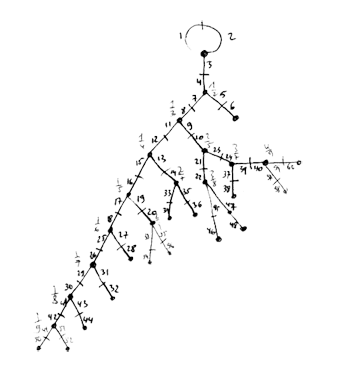 Clearly, I didnt do the calculations in the archaic way of the previous post (as depicted on the left) which consisted in adding a pair of new legs at the proper place in the spine for every new Farey number, write down the two generating permutations, giving them to GAP and check simplicity and the isomorphism type.
Clearly, I didnt do the calculations in the archaic way of the previous post (as depicted on the left) which consisted in adding a pair of new legs at the proper place in the spine for every new Farey number, write down the two generating permutations, giving them to GAP and check simplicity and the isomorphism type.
Instead I used a nice SAGE-package to compute with Farey-symbols written by Chris Kurth and available from his website. As this package is a good tool to experiment hunting for other dinosaur-series of simple groups coming from series of Farey-symbols, Ill include the details for $Ig_3 $ (the example used to outline the construction of the Iguanodon-series ).
First we need to have the n-th Farey-sequence $F(n) $. There are several short Python programs around to do this, for example this one from the Python-Cookbook. Save it to your sage-directory and name it fareyseq.py and load it into sage via load fareyseq.py. Then typing farey(3) to the sage-prompt spits back
sage: farey(3)
[(1, 3), (1, 2), (2, 3)]
That is, 0 and 1 are not included and Farey-numbers are represented by numerator-denominator couples. The iguanodon-series uses the Fareys upto 1/2, identifies the edges connecting 0 and 1 to $\infty $ and makes all other intervals odd. That is, the corresponding Farey symbol for F(3) is
[tex]\xymatrix{\infty \ar@{-}[r]_{1} & 0 \ar@{-}[r]_{\bullet} & \frac{1}{3} \ar@{-}[r]_{\bullet} & \frac{1}{2} \ar@{-}[r]_{\bullet} & 1 \ar@{-}[r]_{1} & \infty}[/tex]
(to add to the confusion, I denote odd intervals by a black-bullet whereas in Kulkarni’s paper they are white…) Anyway, get Kurth’s kfarey-package and save the folder as kfarey in your sage-folder. Kurth uses the following notation for Farey-symbols
The Farey Symbol is a list [a,b,p] where a is a list of numerators, b a list of denominators, and p the pairing information. If x[i]=a[i]/b[i]: inf x0 x1 x2 ... xn inf p0 p1 p2 ... pn pn+1 So p[i] is the pairing of the side between x[i-1] and x[i]. The p[i]’s can be positive integers, indicating pairing between sides, or -2 or -3, meaning an even or odd pairing respectively.
The above Farey-symbol is therefore represented as
[[0,1,1,1],[1,3,2,1],[1,-3,-3,-3,1]]. The kfarey-function LRCosetRep(F) returns two permutations L and R giving the permutation action of the two generators of the modular group $PSL_2(\mathbb{Z}) $
$~~~L = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}~\qquad \text{and} \qquad~R = \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} $
on the half-legs of the inguanodon (the dessin corresponding to the Farey-symbol). Here’s the sage transcript
sage: load kfarey/farey.sage
sage: load kfarey/conggroups.sage
sage: load kfarey/LR.sage
sage: ig3=[[0,1,1,1],[1,3,2,1],[1,-3,-3,-3,1]]
sage: LRCosetRep(ig3)
[(1,2,3,9,10,11,6,7,8,4,5)(12), (1,8,4,2,11,6,3,12,10,7,5)(9)]
Giving these two generators to GAP one verifies that they indeed generate $M_{12} $
gap> ig3:=Group((1,2,3,9,10,11,6,7,8,4,5)(12), (1,8,4,2,11,6,3,12,10,7,5)(9));
Group([ (1,2,3,9,10,11,6,7,8,4,5), (1,8,4,2,11,6,3,12,10,7,5) ])
gap> IsSimpleGroup(ig3);
true
gap> IsomorphismTypeInfoFiniteSimpleGroup(ig3);
rec( series := “Spor”, name := “M(12)” )
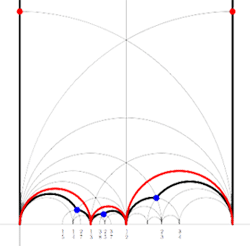

kfarey has plenty of other useful functions. One can even create an .eps file of the fundamental domain specified by the subgroup of the modular group encoded by the Farey symbol using MakeEpsFile(F). For the above example it returns the picture on the right. Not quite as nice as the one on the left, but surely a lot easier to create.
5 Comments