Raymond Smullyan brought Knights and Knaves puzzles to a high art in his books. Here’s the setting:
On Smullyan’s islands there are Knights, who always tell true statements, Knaves, who always lie, and sometimes also Normals, who sometimes tell the truth and sometimes lie.

(image credit MikeKlein)
Problems of this sort can be solved by classical propositional logic, replacing every sentence $P$ told by inhabitant $A$ by the formula $k_A \leftrightarrow P$ where $k_A$ is the sentence “A is a Knight”.
Some time ago I asked for Smullyanesque problems in a non-classical logic, where we replace the usual truth-values $T$ (true) and $F$ (false) of propositional logic by elements of an Heyting algebra.
Jason Rosenhouse wrote a paper Knights, Knaves, Normals, and Neutrals for The College Mathematics Journal, containing more information than in his blog post, as well as some nice challenging puzzles. Here’s Rosenhouse’s setting:
Apart from Knights, Knaves and Normals there’s also the tribe of Neutrals (which he describes as a sort of trans-Knights or trans-Knaves) who can only tell sentences with truth value $N$ in the Heyting algebra $\{ T,N,F \}$ with logical connectives
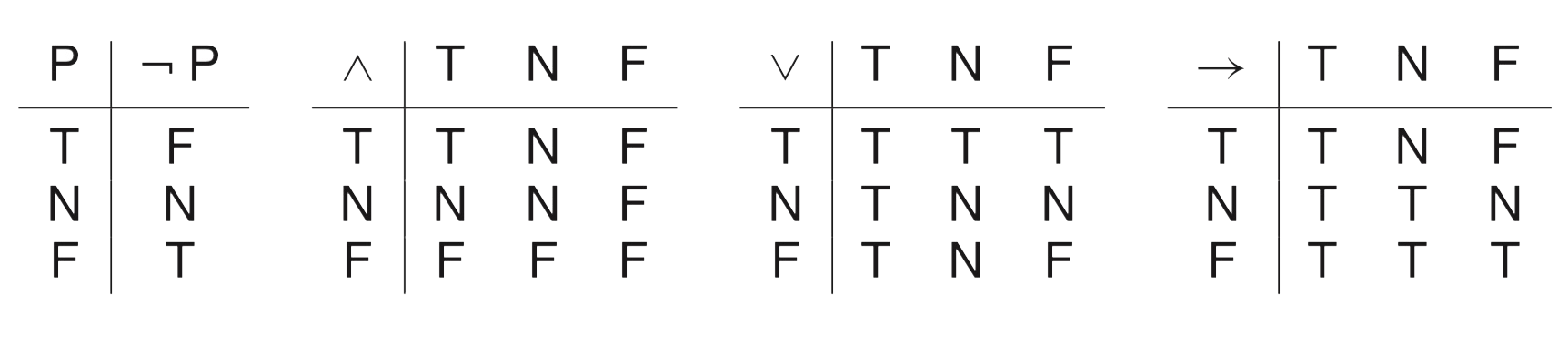
A typical sentence of truth value $N$ is “A is a Knight” or “A is a Knave” whereas, in reality, $A$ is Neutral. Here are the truth values of sentences about a person (the column headings) with respect to the actual situation (the row headings)
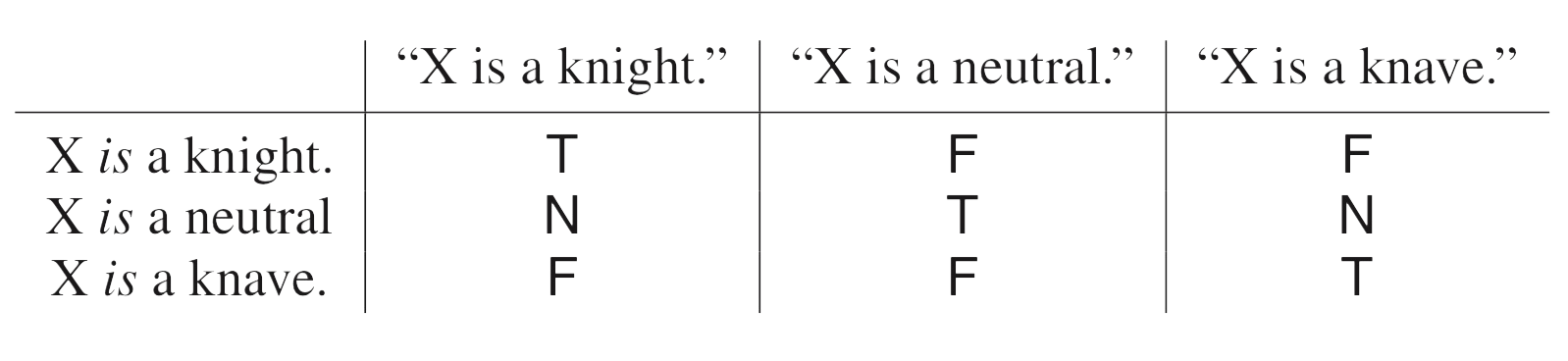
A good way into such problems is to focus on sentence like “A is a Neutral” as they have only classical truth values $T$ or $F$ and to remember that Neutrals can never say a sentence with classical truth value. Here’s an example (only Knights,Knaves or Neutrals present):
Problem 1: Suppose you meet three people, named Dave, Evan and Ford. They make the following statements:
Dave: Evan is a knight.
Evan: Ford is a knave.
Ford: Dave is a neutral.
Can you determine the types of all three people?
Solution: Ford’s sentence has value $T$ or $F$, so Ford cannot be Neutral so must be a Knight or Knave. But then Evan’s sentence also has classical truth value, so he can’t be Neutral either, and by the same reasoning also Dave cannot be neutral. So, we know that all three people must be either Knights or Knaves and then it follows at once that Ford is a Knave (because he lied) and that Evan and Dave must be knights.
These puzzles become more interesting once we use logical connectives.
Problem 2: What can you conclude from this dialog?
Mimi: Olaf is a Knight and Olaf is not a Knight.
Nate: Olaf is a Knave or Olaf is not a Knave.
Olaf: Mimi is a Knight or Nate is a Knave or I am Neutral.
Solution: Mimi’s sentence can only have truth value $F$ or $N$ so she can’t be a Knight. Nate’s sentence has value $T$ or $N$ so he cannot be a Knave.
The two first parts of Olaf’s line cannot be $T$ so must be either $N$ or $F$. So, Olav’s line has total value $T$ only if the last part ‘I am Neutral’ is $T$. So, Olaf can neither be a Knight (because then the last part is $F$) nor Neutral (because then the line would have value $T$ and Neutrals can only speak $N$-sentences). So, Olaf must be a knave. Nate must then be a Knight and Mimi a Knave (because the first part of her line is $F$ and so must be the whole sentence).
The situation becomes even more complicated when we allow Normals (who sometimes lie and sometimes tell the truth but never say sentences with value $N$) to be present. Here’s Rosenhouse’s ‘Grand Finale’:
Problem 3: One day a visitor encountered eight people, among them exactly two Knights, two Knaves, two Normals and two Neutrals. What can you conclude from this dialog:
Sara: Walt is a Neutral or Vera is a Neutral.
Todd: Xara is a Knave and Yoav is a Knave.
Ursa: If Sara is a Knight, then Todd and Yoav are Normals.
Vera: I am not a Neutral.
Walt: If Vera is not a Neutral, then neither is Todd.
Xara: Todd is a Knight if and only if Zack is a Neutral.
Zack: Xara is a Neutral if and only if Walt is not a Normal.
You will solve this problem much quicker than to read through the long explanation in Rosenhouse’s paper.
These puzzles beg to be generalised to more complicated Heyting algebras.
What about a book on “Knights, Knaves and Knols”? A Knol (or $X$-Knol) has knowledge limited to sentences with truth value $X$, an element in the Heyting algebra.
Comments