The sporadic second Janko group $J_2$ is generated by an element of order two and one of order three and hence is a quotient of the modular group $PSL_2(\mathbb{Z}) = C_2 \ast C_3$.
This Janko group has a 100-dimensional permutation representation and hence there is an index 100 subgroup $G$ of the modular group such that the fundamental domain $\mathbb{H}/G$ for the action of $G$ on the upper-half plane by Moebius transformations consists of 100 triangles in the Dedekind tessellation.
Four years ago i tried to depict this fundamental domain in the Farey symbols of sporadic groups-post using Chris Kurth’s kfarey package in Sage, but the result was rather disappointing.
Now, the kfarey-package has been greatly extended by Hartmut Monien of Bonn University and is integrated in the latest version of Sage, SAGE 5.0, released a few weeks ago.
Using the Farey symbol sage-documentation it is easy to repeat the calculations from four years ago and, this time, we do obtain this rather nice picture of the fundamental domain
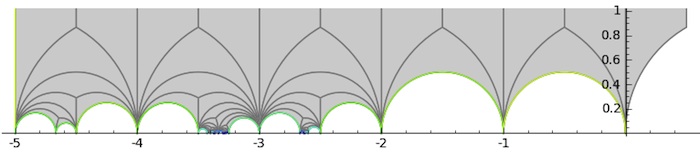
But, there’s a lot more one can do with the new package. By combining the .fractions() with the .pairings() info it is now possible to get the corresponding Farey code which consists of 34 edges, starting off with
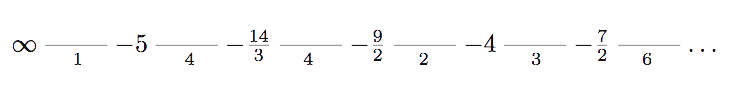
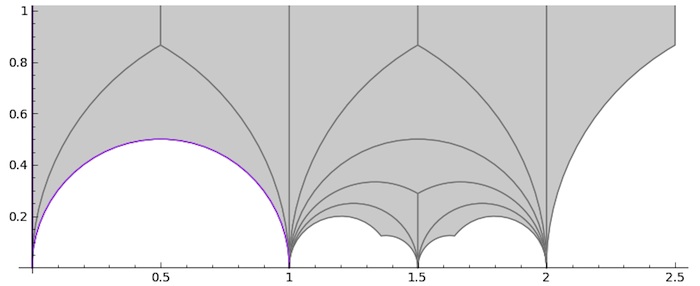
Perhaps surprisingly (?) $G$ turns out to be a genus zero modular subgroup. Naturally, i couldn’t resist drawing the fundamental domain for the 12-dimensional permutations representation of the Mathieu group $M_{12}$ and compare it with that of last time.
Comments