Skip to content →

Category: stories

The best rejected proposal ever

Published March 7, 2007 by lievenlb


The Oscar in
the category The Best Rejected Research Proposal in Mathematics
(ever) goes to … Alexander Grothendieck
for his proposal Esquisse d’un Programme, Grothendieck\’s research program from 1983, written as
part of his application for a position at the CNRS, the French
equivalent of the NSF. An English translation is
available.

Here is one of the problems discussed :
Give TWO non-trivial elements of
$Gal(\overline{\mathbb{Q}}/\mathbb{Q}) $ the _absolute_
Galois group of the algebraic closure of the rational numbers
$\overline{\mathbb{Q}} $, that is the group of all
$\mathbb{Q} $-automorphisms of $\overline{\mathbb{Q}} $. One element
most of us can give (complex-conjugation) but to find any other
element turns out to be an extremely difficult task.

To get a handle on
this problem, Grothendieck introduced his _’Dessins d’enfants’_
(Children’s drawings). Recall from last session the pictures of the
left and right handed Monsieur Mathieu

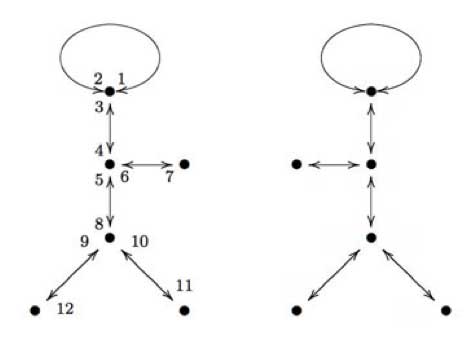
The left hand side drawing was associated to a map
$\mathbb{P}^1_{\mathbb{C}} \rightarrow \mathbb{P}^1_{\mathbb{C}} $ which was
defined over the field $\mathbb{Q} \sqrt{-11} $ whereas the right side
drawing was associated to the map given when one applies to all
coefficients the unique non-trivial automorphism in the Galois group
$Gal(\mathbb{Q}\sqrt{-11}/\mathbb{Q}) $ (which is
complex-conjugation). Hence, the Galois group
$Gal(\mathbb{Q}\sqrt{-11}/\mathbb{Q}) $ acts _faithfully_ on the
drawings associated to maps $\mathbb{P}^1_{\mathbb{Q}\sqrt{-11}} \rightarrow
\mathbb{P}^1_{\mathbb{Q}\sqrt{-11}} $ which are ramified only over
the points ${ 0,1,\infty } $.

Grothendieck’s idea was to
extend this to more general maps. Assume that a projective smooth curve
(a Riemann surface) X is defined over the algebraic numbers
$\overline{\mathbb{Q}} $ and assume that there is a map $X
\rightarrow \mathbb{P}^1_{\mathbb{C}} $ ramified only over the points
${ 0,1,\infty } $, then we can repeat the procedure of last time and
draw a picture on X consisting of d edges (where d is the degree
of the map, that is the number of points lying over another point of
$\mathbb{P}^1_{\mathbb{C}} $) between white resp. black points (the
points of X lying over 1 (resp. over 0)).

Call such a drawing a
‘dessin d\’enfant’ and look at the collection of ALL dessins
d’enfants associated to ALL such maps where X runs over ALL curves
defined over $\overline{\mathbb{Q}} $. On this set, there is an action
of the absolute Galois group
$Gal(\overline{\mathbb{Q}}/\mathbb{Q}) $ and if this action would be
faithful, then this would give us insight into this
group. However, at that time even the existence of a map $X \rightarrow
\mathbb{P}^1 $ ramified in the three points ${ 0,1,\infty } $
seemed troublesome to prove, as Grothendieck recalls in his proposal

In more erudite terms, could it be true that
every projective non-singular algebraic curve defined over a number
field occurs as a possible ‚ modular curve‚ parametrising
elliptic curves equipped with a suitable rigidification? Such a
supposition seemed so crazy that I was almost embarrassed to submit
it to the competent people in the domain. Deligne when I consulted
him found it crazy indeed, but didn’t have any counterexample up
his sleeve. Less than a year later, at the International Congress in
Helsinki, the Soviet mathematician Bielyi announced exactly that result,
with a proof of disconcerting simplicity which fit into two little
pages of a letter of Deligne ‚ never, without a doubt, was such a
deep and disconcerting result proved in so few lines!

In
the form in which Bielyi states it, his result essentially says that
every algebraic curve defined over a number field can be obtained as
a covering of the projective line ramified only over the points 0,
1 and infinity. This result seems to have remained more or less
unobserved. Yet, it appears to me to have considerable importance. To
me, its essential message is that there is a profound identity
between the combinatorics of finite maps on the one hand, and the
geometry of algebraic curves defined over number fields on the
other. This deep result, together with the algebraic- geometric
interpretation of maps, opens the door onto a new, unexplored world within reach of all, who pass by without seeing it.

Belyi’s proof is indeed relatively easy
(full details can be found in the paper Dessins d’enfants on the
Riemann sphere by Leila
Schneps). Roughly it goes as follows : as both X and the map are
defined over $\overline{\mathbb{Q}} $ the map is only ramified over
(finitely many) $\overline{\mathbb{Q}} $-points. Let S be the finite
set of all Galois-conjugates of these points and consider the polynomial

$f_0(z_0) = \prod_{s \in S} (z_0 -s) \in
\mathbb{Q}[z_0] $

Now, do a
resultant trick. Consider the
polynomial $f_1(z_1) = Res_{z_0}(\frac{d f_0}{d
z_0},f_0(z_0)-z_1) $ then the roots of $f_1(z_1) $ are exactly the
finite critical values of $f_0 $, $f_1 $ is again defined over
$\mathbb{Q} $ and has lower degree (in $z_1 $) than $f_0 $ in $z_1 $.
Continue this trick a finite number of times untill you have constructed
a polynomial $f_n(z_n) \in \mathbb{Q}[z_n] $ of degree zero.

Composing
the original map with the maps $f_j $ in succession yields that all
ramified points of this composition are
$\mathbb{Q} $-points! Now, we only have to limit the number of
these ramified $\mathbb{Q} $-points (let us call this set T) to three.

Take any three elements of T, then there always exist integers $m,n
\in \mathbb{Z} $ such that the three points go under a linear
fractional transformation (a Moebius-function associated to a matrix in
$PGL_2(\mathbb{Q}) $) to ${ 0,\frac{m}{m+n},1 } $. Under the
transformation $z \rightarrow \frac{(m+n)^{m+n}}{m^m
n^n}z^m(1-z)^n $ the points 0 and 1 go to 0 and
$\frac{m}{m+n} $ goes to 1 whence the ramified points of the
composition are one less in number than T. Continuing in this way we
can get the set of ramified $\mathbb{Q} $-points of a composition at
most having three elements and then a final Moebius transformation gets
them to ${ 0,1,\infty } $, done!

As a tribute for this clever
argument, maps $X \rightarrow \mathbb{P}^1 $ ramified only in 0,1 and
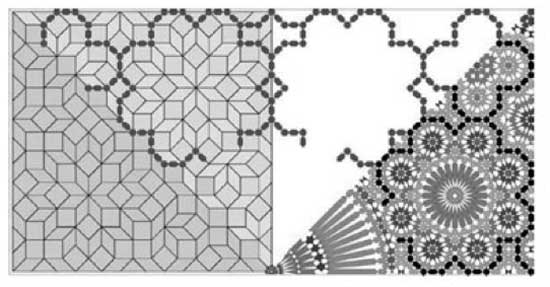
$\infty $ are now called Belyi morphisms. Here is an example of
a Belyi-morphism (and the corresponding dessin d’enfants) associated to
one of the most famous higher genus curves around : the Klein
quartic (if you haven’t done
so yet, take your time to go through this marvelous pre-blog post by
John Baez).

One can define the Klein quartic as the plane projective
curve K with defining equation in
$\mathbb{P}^2_{\\mathbb{C}} $ given by $X^3Y+Y^3Z+Z^3X = 0 $ K has
a large group of automorphism, namely the simple group of order
168 $G = PSL_2(\mathbb{F}_7) =
SL_3(\mathbb{F}_2) $ It is a classical fact (see for example
the excellent paper by Noam Elkies The Klein quartic in number theory) that the quotient map $K \rightarrow K/G =
\mathbb{P}^1_{\mathbb{C}} $ is ramified only in the points
0,1728 and $\infty $ and the number of points of K lying over them
are resp. 56, 84 and 24. Now, compose this map with the Moebius
transormation taking ${ 0,1728,\infty } \rightarrow { 0,1,\infty } $
then the resulting map is a Belyi-map for the Klein quartic. A
topological construction of the Klein quartic is fitting 24 heptagons
together so that three meet in each vertex, see below for the gluing
data-picture in the hyperbolic plane : the different heptagons are given
a number but they appear several times telling how they must fit
together)

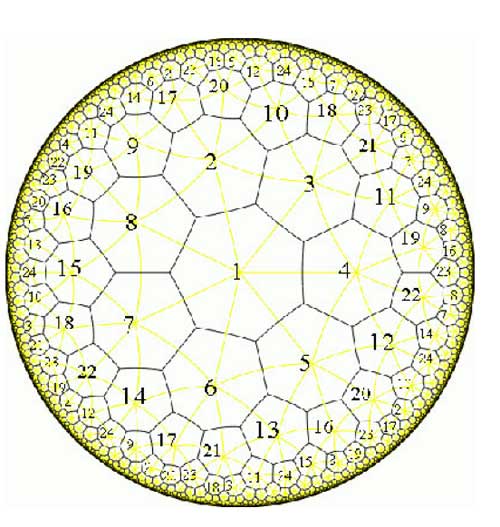
The resulting figure has exactly $\frac{7 \times 24}{2} =
84 $ edges and the 84 points of K lying over 1 (the white points in
the dessin) correspond to the midpoints of the edges. There are exactly
$\frac{7 \times 24}{3}=56 $ vertices corresponding to the 56 points
lying over 0 (the black points in the dessin). Hence, the dessin
d\’enfant associated to the Klein quartic is the figure traced out by
the edges on K. Giving each of the 168 half-edges a
different number one assigns to the white points a permutation of order
two and to the three-valent black-points a permutation of order three,
whence to the Belyi map of the Klein quartic corresponds a
168-dimensional permutation representation of $SL_2(\mathbb{Z}) $,
which is not so surprising as the group of automorphisms is
$PSL_2(\mathbb{F}_7) $ and the permutation representation is just the
regular representation of this group.

Next time we will see how
one can always associate to a curve defined over
$\overline{\mathbb{Q}} $ a permutation representation (via the Belyi
map and its dessin) of one of the congruence subgroups $\Gamma(2) $ or
$\Gamma_0(2) $ or of $SL_2(\mathbb{Z}) $ itself.

6 Comments

the father of all beamer talks

Published March 2, 2007 by lievenlb

Who was the first mathematician to give a slide show talk? I don’t have the
definite answer to this question, but would like to offer a strong
candidate : Hermann Minkowski gave the talk “Zur Geometrie der Zahlen” (On the
geometry of numbers) before the third ICM in 1904 in Heidelberg and even
the title page of his paper in the proceedings indicates that he did
present his talk using slides (Mit Projektionsbildern auf einer
Doppeltafel)

Seven
of these eight slides would be hard to improve using LaTeX

What concerns
us today is the worst of all slides, the seventh, where Minkowski tries
to depict his famous questionmark function $?(x) $, sometimes also called
the _devil’s staircase_

The devil’s
staircase is a fractal curve and can be viewed as a mirror (taking a
point on the horizontal axis to the point on the vertical axis through
the function value) having magical simplifying properties : – it takes
rational numbers to _dyadic numbers_, that is those of the form
$n.2^{-m}$ with $n,m \in \mathbb{Z} $. – it takes quadratic
_irrational_ numbers to rational numbers. So, iterating this
mirror-procedure, the devil’s staircase is a device solving the main
problem of Greek Mathematics : which lengths can be constructed using
ruler and compass? These _constructible numbers_ are precisely those
real numbers which become after a finite number of devil-mirrors a
dyadic number. The proofs of these facts are not very difficult but
they involve a piece of long-forgotten mathematical technology :
_continued fractions_. By repeted approximations using the
floor-function (the largest natural number less than or equal to the real
number), every positive real number can be written as

$a = a_0 +
\frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{a_3 + \frac{1}{\dots}}}} $

with all $a_i $ natural numbers. So, let us just denote from now on this
continued fraction of a by the expression

$a = \langle
a_0;a_1,a_2,a_3,\dots \rangle $

Clearly, a is a rational number if
(and also if but this requires a small argument using the Euclidian
algorithm) the above description has a tail of zeroes at the end and
(slightly more difficult) $a$ is a real quadratic irrational number
(that is, an element of a quadratic extension field
$\mathbb{Q}\sqrt{n} $) if and only if the continued fraction-expression
has a periodic tail. There is a lot more to say about
continued-fraction expressions and I’ll do that in another
‘virtual-course-post’ (those prepended with a (c): sign). For the
impatient let me just say that two real numbers will lie in the same
$GL_2(\mathbb{Z}) $-orbit (under the action via Moebius-transformations)
if and only if their continued fraction expressions have the same tails
eventually (which has applications in noncommutative geometry as in the
work of Manin and Marcolli but maybe I’ll come to this in the (c):
posts).

Right, now we can define the mysterious devil-stair function
$?(x) $. If a is in the real interval $[0,1] $ and if $a \in
\mathbb{Q} $ then $a = \langle 0;a_1,a_2,\dots,a_n,0,0,\dots
\rangle $ and we define $?(a) = 2 \sum_{k=1}^{n} (-1)^k
2^{-(a_1+a_2+\dots+a_k)} $ and if a is irrational with continued
fraction expression $a = \langle 0;a_1,a_2,a_3,\dots \rangle $, then

$?(a) = 2 \sum_{k=1}^{\infty} (-1)^{k+1} 2^{-(a_1+a_2+\dots+a_k)} $

A
perhaps easier description is that with the above continued-fraction
expression, the _binary_ expansion of $?(a) $ has the following form

$?(a) = 0,0 \dots 01 \dots 1 0 \dots 0 1 \dots 1 0 \dots 0 1 \dots
1 0 \dots $

where the first batch of zeroes after the comma has length
$a_1-1 $, the first batch of ones has length $a_2 $ the next batch of
zeroes length $a_3 $ and so on.

It is a pleasant exercise to verify that
this function does indeed have the properties we claimed before. A
recent incarnation of the question mark function is in Conway’s game of
_contorted fractions_. A typical position consists of a finite number of
boxed real numbers, for example the position might be

$\boxed{\pi} + \boxed{\sqrt{2}} + \boxed{1728} +
\boxed{-\frac{1}{3}} $

The Rules of the game are : (1) Both
players L and R take turns modifying just one of the numbers such that
the denominator becomes strictly smaller (irrational numbers are
supposed to have $\infty$ as their ‘denominator’). And if the boxed
number is already an integer, then its absolute value must decrease.
(2) Left must always _decrease_ the value of the boxed number, Right
must always increase it. (3) The first player unable to move looses
the game. To decide who wins a particular game, one needs to compute
the value of a position $\boxed{x} $ according to the rules of
combinatorial game theory (see for example the marvelous series of four
books Winning Ways for your Mathematical Plays. It turns out that this CG-value is no other than $?(x)$
… And, Conway has a much improved depiction of the devil-staircase in
his book On Numbers And Games

One Comment

noncommutative geometry : a medieval science?

Published February 28, 2007 by lievenlb

According to a science article in the New York Times, archeologists have discovered “signs of advanced math” in medieval mosaics. An example of a quasi-crystalline Penrose pattern was found at the Darb-i Imam shrine in Isfahan, Iran.

“A new study shows that the Islamic pattern-making process, far more intricate than the laying of one‚Äôs bathroom floor, appears to have involved an advanced math of quasi crystals, which was not understood by modern scientists until three decades ago. Two years ago, Peter J. Lu, a doctoral student in physics at Harvard University, was transfixed by the geometric pattern on a wall in Uzbekistan. It reminded him of what mathematicians call quasi-crystalline designs. These were demonstrated in the early 1970s by Roger Penrose, a mathematician and cosmologist at the University of Oxford. Mr. Lu set about examining pictures of other tile mosaics from Afghanistan, Iran, Iraq and Turkey, working with Paul J. Steinhardt, a Princeton cosmologist who is an authority on quasi crystals and had been Mr. Lu’s undergraduate adviser. ”

Penrose tilings are one of the motivating examples of Alain Connes’ book as there is a $C^* $-algebra associated to it. In fact, the algebra is AF ( a limit of semi-simple finite dimensional algebras) so is even a formally smooth algebra in Kontsevichian noncommutative geometry (it is remarkable how quickly one gets used to silly terminology…). However, the Penrose algebra is simple, so rather useless from the point of view of finite dimensional representations… Still, Connesian noncommutative geometry may be a recent incarnation of the medieval Tehran program (pun intended). Thanks to easwaran for the link (via Technorati).

Added, March 1 : I haven’t looked at the Connes-Marcolli paper A walk in the noncommutative garden for a while but now that I do, I see that they mentioned the above already at the end of their section on Tilings (page 32). They also include clearer pictures.


One Comment