Skip to content →

Category: stories

Art and the absolute point (2)

Published May 13, 2011 by lievenlb

Last time we did recall Manin’s comparisons between some approaches to geometry over the absolute point $\pmb{spec}(\mathbb{F}_1)$ and trends in the history of art.

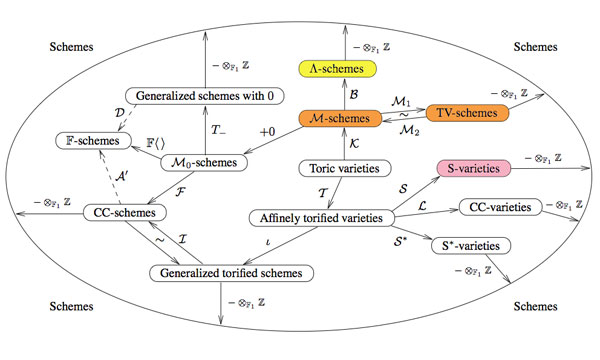
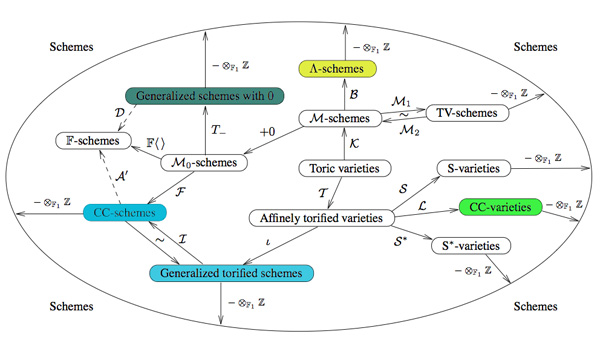
In the comments to that post, Javier Lopez-Pena wrote that he and Oliver Lorscheid briefly contemplated the idea of extending Manin’s artsy-dictionary to all approaches they did draw on their Map of $\mathbb{F}_1$-land.

So this time, we will include here Javier’s and Oliver’s insights on the colored pieces below in their map : CC=Connes-Consani, Generalized torified schemes=Lopez Pena-Lorscheid, Generalized schemes with 0=Durov and, this time, $\Lambda$=Manin-Marcolli.

Durov : romanticism

In his 568 page long Ph.D. thesis New Approach to Arakelov Geometry Nikolai Durov introduces a vast generalization of classical algebraic geometry in which both Arakelov geometry and a more exotic geometry over $\mathbb{F}_1$ fit naturally. Because there were great hopes and expectations it would lead to a big extension of algebraic geometry, Javier and Oliver associate this approach to romantism. From wikipedia : “The modern sense of a romantic character may be expressed in Byronic ideals of a gifted, perhaps misunderstood loner, creatively following the dictates of his inspiration rather than the standard ways of contemporary society.”

Manin and Marcolli : impressionism

Yuri I. Manin in Cyclotomy and analytic geometry over $\mathbb{F}_1$ and Matilde Marcolli in Cyclotomy and endomotives develop a theory of analytic geometry over $\mathbb{F}_1$ based on analytic functions ‘leaking out of roots of unity’. Javier and Oliver depict such functions as ‘thin, but visible brush strokes at roots of 1’ and therefore associate this approach to impressionism. Frow wikipedia : ‘Characteristics of Impressionist paintings include: relatively small, thin, yet visible brush strokes; open composition; emphasis on accurate depiction of light in its changing qualities (often accentuating the effects of the passage of time); common, ordinary subject matter; the inclusion of movement as a crucial element of human perception and experience; and unusual visual angles.’

Connes and Consani : cubism

In On the notion of geometry over $\mathbb{F}_1$ Alain Connes and Katia Consani develop their extension of Soule’s approach. A while ago I’ve done a couple of posts on this here, here and here. Javier and Oliver associate this approach to cubism (a.o. Pablo Picasso and Georges Braque) because of the weird juxtapositions of the simple monoidal pieces in this approach.

Lopez-Pena and Lorscheid : deconstructivism

Torified varieties and schemes were introduced by Javier Lopez-Pena and Oliver Lorscheid in Torified varieties and their geometries over $\mathbb{F}_1$ to get lots of examples of varieties over the absolute point in the sense of both Soule and Connes-Consani. Because they were fragmenting schemes into their “fundamental pieces” they associate their approach to deconstructivism.

Another time I’ll sketch my own arty-farty take on all this.

Leave a Comment

Art and the absolute point

Published May 12, 2011 by lievenlb

In his paper Cyclotomy and analytic geometry over $\mathbb{F}_1$ Yuri I. Manin sketches and compares four approaches to the definition of a geometry over $\mathbb{F}_1$, the elusive field with one element.

He writes : “Preparing a colloquium talk in Paris, I have succumbed to the temptation to associate them with some dominant trends in the history of art.”

Remember that the search for the absolute point $\pmb{spec}(\mathbb{F}_1)$ originates from the observation that $\pmb{spec}(\mathbb{Z})$, the set of all prime numbers together with $0$, is too large to serve as the terminal object in Grothendieck’s theory of commutative schemes. The last couple of years have seen a booming industry of proposals, to the extent that Javier Lopez Pena and Oliver Lorscheid decided they had to draw a map of $\mathbb{F}_1$-land.

Manin only discusses the colored proposals (TV=Toen-Vaquie, M=Deitmar, S=Soule and $\Lambda$=Borger) and compares them to these art-history trends.

Toen and Vaquie : Abstract Expressionism

In Under $\pmb{spec}(\mathbb{Z})$ Bertrand Toen and Michel Vaquie argue that geometry over $\mathbb{F}_1$ is a special case of algebraic geometry over a symmetric monoidal category, taking the simplest example namely sets and direct products. Probably because of its richness and abstract nature, Manin associates this approach to Abstract Expressionism (a.o. Karel Appel, Jackson Pollock, Mark Rothko, Willem de Kooning).

Deitmar : Minimalism

Because monoids are the ‘commutative algebras’ in sets with direct products, an equivalent proposal is that of Anton Deitmar in Schemes over $\mathbb{F}_1$ in which the basic affine building blocks are spectra of monoids, topological spaces whose points are submonoids satisfying a primeness property. Because Deitmar himself calls this approach a ‘minimalistic’ one it is only natural to associate to it Minimalism where the work is stripped down to its most fundamental features. Prominent artists associated with this movement include Donald Judd, John McLaughlin, Agnes Martin, Dan Flavin, Robert Morris, Anne Truitt, and Frank Stella.

Soule : Critical Realism

in Les varietes sur le corps a un element Christophe Soule defines varieties over $\mathbb{F}_1$ to be specific schemes $X$ over $\mathbb{Z}$ together with a form of ‘descent data’ as well as an additional $\mathbb{C}$-algebra, morally the algebra of functions on the real place. Because of this Manin associates to it Critical Realism in philosophy. There are also ‘realism’ movements in art such as American Realism (o.a. Edward Hopper and John Sloan).

Borger : Futurism

James Borger’s paper Lambda-rings and the field with one element offers a totally new conception of the descent data from $\mathbb{Z}$ to $\mathbb{F}_1$, namely that of a $\lambda$-ring in the sense of Grothendieck. Because Manin expects this approach to lead to progress in the field, he connects it to Futurism, an artistic and social movement that originated in Italy in the early 20th century.

4 Comments

the Reddit (after)effect

Published January 15, 2011 by lievenlb

Sunday january 2nd around 18hr NeB-stats went crazy.

Referrals clarified that the post ‘What is the knot associated to a prime?’ was picked up at Reddit/math and remained nr.1 for about a day.

Now, the dust has settled, so let’s learn from the experience.

A Reddit-mention is to a blog what doping is to a sporter.

You get an immediate boost in the most competitive of all blog-stats, the number of unique vistors (blue graph), but is doesn’t result in a long-term effect, and, it may even be harmful to more essential blog-stats, such as the average time visitors spend on your site (yellow graph).

For NeB the unique vistors/day fluctuate normally around 300, but peaked to 1295 and 1733 on the ‘Reddit-days’. In contrast, the avg. time on site is normally around 3 minutes, but dropped the same days to 44 and 30 seconds!

Whereas some of the Reddits spend enough time to read the post and comment on it, the vast majority zap from one link to the next. Having monitored the Reddit/math page for two weeks, I’m convinced that post only made it because it was visually pretty good. The average Reddit/math-er is a viewer more than a reader…

So, should I go for shorter, snappier, more visual posts?

Let’s compare Reddits to those coming from the three sites giving NeB most referrals : Google search, MathOverflow and Wikipedia.

This is the traffic coming from Reddit/math, as always the blue graph are the unique visitors, the yellow graph their average time on site, blue-scales to the left, yellow-scales to the right.

Here’s the same graph for Google search. The unique visitors/day fluctuate around 50 and their average time on site about 2 minutes.

The math-related search terms most used were this month : ‘functor of point approach’, ‘profinite integers’ and ‘bost-connes sytem’.

More rewarding to me are referrals from MathOverflow.

The number of visitors depends on whether the MathO-questions made it to the front-page (for example, the 80 visits on december 15, came from the What are dessins d’enfants?-topic getting an extra comment that very day, and having two references to NeB-posts : The best rejected proposal ever and Klein’s dessins d’enfant and the buckyball), but even older MathO-topics give a few referrals a day, and these people sure take their time reading the posts (+ 5 minutes).

Other MathO-topics giving referrals this month were Most intricate and most beautiful structures in mathematics (linking to Looking for F-un), What should be learned in a first serious schemes course? (linking to Mumford’s treasure map (btw. one of the most visited NeB-posts ever)), How much of scheme theory can you visualize? (linking again to Mumford’s treasure map) and Approaches to Riemann hypothesis using methods outside number theory (linking to the Bost-Connes series).

Finally, there’s Wikipedia

giving 5 to 10 referrals a day, with a pretty good time-on-site average (around 4 minutes, peaking to 12 minutes). It is rewarding to see NeB-posts referred to in as diverse Wikipedia-topics as ‘Fifteen puzzle’, ‘Field with one element’, ‘Evariste Galois’, ‘ADE classification’, ‘Monster group’, ‘Arithmetic topology’, ‘Dessin d’enfant’, ‘Groupoid’, ‘Belyi’s theorem’, ‘Modular group’, ‘Cubic surface’, ‘Esquisse d’un programme’, ‘N-puzzle’, ‘Shabat polynomial’ and ‘Mathieu group’.

What lesson should be learned from all this data? Should I go for shorter, snappier and more visual posts, or should I focus on the small group of visitors taking their time reading through a longer post, and don’t care about the appallingly high bounce rate the others cause?

8 Comments