Skip to content →

Category: featured

“God given time”

Published February 20, 2008 by lievenlb

If you ever sat through a lecture by Alain Connes you will know about his insistence on the ‘canonical dynamic nature of noncommutative manifolds’. If you haven’t, he did write a blog post Heart bit 1 about it.

I’ll try to explain here that there is a definite “supplément d’âme” obtained in the transition from classical (commutative) spaces to the noncommutative ones. The main new feature is that “noncommutative spaces generate their own time” and moreover can undergo thermodynamical operations such as cooling, distillation etc…

Here a section from his paper A view of mathematics :

Indeed even at the coarsest level of understanding of a space provided by measure
theory, which in essence only cares about the “quantity of points” in a space, one
finds unexpected completely new features in the noncommutative case. While it
had been long known by operator algebraists that the theory of von-Neumann
algebras represents a far reaching extension of measure theory, the main surprise
which occurred at the beginning of the seventies is that such an algebra M
inherits from its noncommutativity a god-given time evolution:

$\delta~:~\mathbb{R} \rightarrow Out(M) $

where $Out M = Aut M/Int M $ is the quotient of the group of automorphisms of M
by the normal subgroup of inner automorphisms. This led in my thesis to the
reduction from type III to type II and their automorphisms and eventually to the
classification of injective factors.

Even a commutative manifold has a kind of dynamics associated to it. Take a suitable vectorfield, consider the flow determined by it and there’s your ‘dynamics’, or a one-parameter group of automorphisms on the functions. Further, other classes of noncommutative algebras have similar features. For example, Cuntz and Quillen showed that also formally smooth algebras (the noncommutative manifolds in the algebraic world) have natural Yang-Mills flows associated to them, giving a one-parameter subgroup of automorphisms.

Let us try to keep far from mysticism and let us agree that by ‘time’ (let alone ‘god given time’) we mean a one-parameter subgroup of algebra automorphisms of the noncommutative algebra. In nice cases, such as some von-Neumann algebras this canonical subgroup is canonical in the sense that it is unique upto inner automorphisms.

In the special case of the Bost-Connes algebra these automorphisms $\sigma_t $ are given by $\sigma_t(X_n) = n^{it} X_n $ and $\sigma_t(Y_{\lambda}) = Y_{\lambda} $.

This one-parameter subgroup is crucial in the definition of the so called KMS-states (for Kubo-Martin and Schwinger) which is our next goal.

2 Comments

music of the primes (1)

Published February 13, 2008 by lievenlb

This semester, I’m running a 3rd year course on Marcus du Sautoy’s The music of the primes. The concept being that students may suggest topics, merely sketched in the book, and then we’ll go a little deeper into them.

I’ve been rather critical about the book before, but, rereading it last week (and knowing a bit better the limitations of bringing mathematics to the masses…) I think du Sautoy did a great job. Sure, it focusses too much on people and places and too little on mathematics, but that goes with the format.

I wanted to start off gently by playing the open-university dvd-series so that students would have a very rough outline of the book from the very start (as well as a mental image to some of the places mentioned, such as Bletchley Park, the IAS, Gottingen…). However, the vagueness of it all seemed to work on their nerves … in particular the trumpet scenes

Afterwards, they demanded that I should explain next week what on earth the zeroes of the Riemann zeta function had to do with counting primes and what all this nonsensical ‘music of the primes’ was about.

Well, here is the genuine music of the primes (taken from the Riemann page by Jeffrey Stopple whose excellent introductory text A Primer of Analytic Number Theory I’ll use to show them some concrete stuff (they have their first course on complex analysis also this semester, so I cannot go too deep into it).




Jeffrey writes “This sound is best listened to with headphones or external speakers. For maximum effect, play it LOUD.” But, what is the story behind it?

The Von Mangoldt function $\Lambda(n) $ assigns $log(p) $ whenever $n=p^k $ is a prime power and zero otherwise. One can then consider the function

$\Psi(x) = \frac{1}{2}(\sum_{n < x} \Lambda(n) + \sum_{n \leq x} \Lambda(n)) $

which makes a jump at prime power values and the jump-size depends on the prime. Here is a graph of its small values

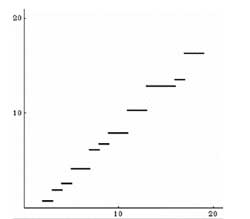It’s not quite the function $\pi(x) $ (counting the number of primes smaller than x) but it sure contains enough information to obtain this provided we have a way of describing $\Psi(x) $.

The Riemann zeta function (or rather $~(s-1)\zeta(s) $) has two product descriptions, the Hadamard product formula (running over all zeroes, both the trivial ones at $-2n $ and those in the critical strip), which is valid for all complex s and the Euler product valid for all $Re(s) > 1 $. This will allow us to calculate in two different ways $\zeta'(s)/\zeta(s) $ which in turn allows us to have an explicit description of $\Psi(s) $ known as the Von Mangoldt formula

$\Psi(x) = x – \frac{1}{2}log(1 – \frac{1}{x^2}) – log(2 \pi) – \sum_{\rho} \frac{x^{\rho}}{\rho} $

where only the last term depends on the zeta-zeroes $\rho $ lying in the critical strip (and conjecturally all lying on the line $Re(x) = \frac{1}{2} $. The first few terms (those independent of the zeroes) give a continuous approximation of $\Psi(x) $ but how on earth can we get from that approxamation (on the left) to the step-like function itself (on the right)?



We can group together zeta-zeroes $\rho=\beta + i \gamma $ with their comlex conjugate zeroes $\overline{\rho} $ and then one shows that the attribution to the Von Mangoldt formula is

$\frac{x^{\rho}}{\rho} + \frac{x^{\overline{\rho}}}{\overline{rho}} = \frac{2 x^{\beta}}{| \rho | }cos(\gamma log(x) – arctan(\gamma/\beta)) $

Ignoring the term $x^{\beta} $ this is a peridodic function with amplitude $2/| \rho | $ (so getting smaller for larger and larger zeroes) and period $2\pi/ \gamma $. If the Riemann hypothesis holds (meaning that $\beta=1/2 $ for all zeroes) one can even split a term in this contribution of every zero as a sort of ‘universal amplitude’. What is left is then a sum of purely periodic functions which a physicist will view as a superposition of (sound) waves and that is the music played by the primes!

Below, a video of the influence of adding the first 100 zeroes to a better and better approximation of $\Psi(x) $ (again taken from the Riemann page by Jeffrey Stopple). Surely watching the video will convince anyone of the importance of the Riemann zeta-zeroes to the prime-counting problem..




One Comment

768 micro-sudokubes

Published February 4, 2008 by lievenlb

Ibrahim Belkadi, one of my first-year group theory students invented the micro-sudokube, that is, a cube having a solution to a micro-sudoku on all its sides such that these solutions share one row along an edge. For example, here are all the solutions for a given central solution. There are 4 of them with ${ a,b } = { 2,3 } $ and ${ c,d } = { 1,4 } $

The problem is : how many micro-sudokubes are there? Ibrahim handed in his paper and claims that there are exactly 32 of them, up to relabeling ${ 1,2,3,4 } $, so in all there are $32 \times 24 = 768 $ micro-sudokubes.

The proof-strategy is as follows. Fix one side and use relabeling to put the solution on that side to be one of 12 canonical forms (see for example this post. Next, work out as above for each of these standard forms in how many ways it can be extended. A nice idea of Ibrahim was to develop a much better notation for micro-sudokubes than the above flattenet-out cube. He uses the fact that a micro-sudokube is entirely determined by the solutions on two opposite sides (check this for yourself). Moreover, fixing one side determines one-half of all the neighboring sides. His notation for the 4 solutions above then becomes

and he can then use these solutions also in other standard form (the extra notation using the names A,B,C 1-4 for the 12 canonical forms).

2 Comments