Skip to content →

Category: featured

the McKay-Thompson series

Published March 22, 2008 by lievenlb

Monstrous moonshine was born (sometime in 1978) the moment John McKay realized that the linear term in the j-function

$j(q) = \frac{1}{q} + 744 + 196884 q + 21493760 q^2 + 864229970 q^3 + \ldots $

is surprisingly close to the dimension of the smallest non-trivial irreducible representation of the monster group, which is 196883. Note that at that time, the Monster hasn’t been constructed yet, and, the only traces of its possible existence were kept as semi-secret information in a huge ledger (costing 80 pounds…) kept in the Atlas-office at Cambridge. Included were 8 huge pages describing the character table of the monster, the top left fragment, describing the lower dimensional irreducibles and their characters at small order elements, reproduced below

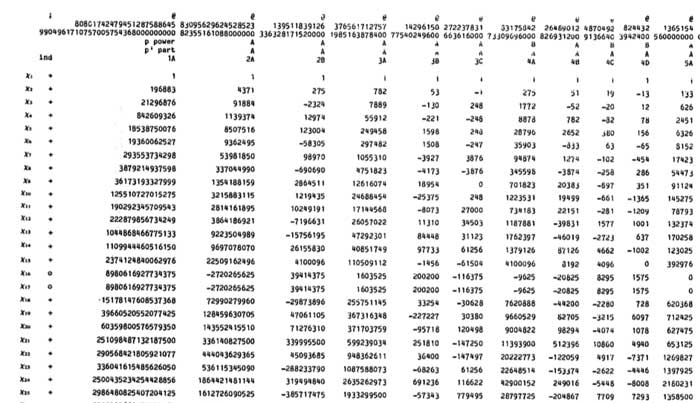
If you look at the dimensions of the smallest irreducible representations (the first column) : 196883, 21296876, 842609326, … you will see that the first, second and third of them are extremely close to the linear, quadratic and cubic coefficient of the j-function. In fact, more is true : one can obtain these actual j-coefficients as simple linear combination of the dimensions of the irrducibles :

$\begin{cases} 196884 &= 1 + 196883 \\
21493760 &= 1 + 196883 + 21296876 \\
864229970 &= 2 \times 1 + 2 \times 196883 + 21296876 + 842609326
\end{cases} $

Often, only the first relation is attributed to McKay, whereas the second and third were supposedly discovered by John Thompson after MKay showed him the first. Marcus du Sautoy tells a somewhat different sory in Finding Moonshine :

McKay has also gone on to find these extra equations, but is was Thompson who first published them. McKay admits that “I was a bit peeved really, I don’t think Thompson quite knew how much I knew.”

By the work of Richard Borcherds we now know the (partial according to some) explanation behind these numerical facts : there is a graded representation $V = \oplus_i V_i $ of the Monster-group (actually, it has a lot of extra structure such as being a vertex algebra) such that the dimension of the i-th factor $V_i $ equals the coefficient f $q^i $ in the j-function. The homogeneous components $V_i $ being finite dimensional representations of the monster, they decompose into the 194 irreducibles $X_j $. For the first three components we have the decompositions

$\begin{cases} V_1 &= X_1 \oplus X_2 \\
V_2 &= X_1 \oplus X_2 \oplus X_3 \\
V_3 &= X_1^{\oplus 2 } \oplus X_2^{\oplus 2} \oplus X_3 \oplus X_4
\end{cases} $

Calculating the dimensions on both sides give the above equations. However, being isomorphisms of monster-representations we are not restricted to just computing the dimensions. We might as well compute the character of any monster-element on both sides (observe that the dimension is just the character of the identity element). Characters are the traces of the matrices describing the action of a monster-element on the representation and these numbers fill the different columns of the character-table above.

Hence, the same integral combinations of the character values of any monster-element give another q-series and these are called the McKay-Thompson series. John Conway discovered them to be classical modular functions known as Hauptmoduln.

In most papers and online material on this only the first few coefficients of these series are documented, which may be just too little information to make new discoveries!

Fortunately, David Madore has compiled the first 3200 coefficients of all the 172 monster-series which are available in a huge 8Mb file. And, if you really need to have more coefficients, you can always use and modify his moonshine python program.

In order to reduce bandwidth, here a list containing the first 100 coefficients of the j-function

jfunct=[196884, 21493760, 864299970, 20245856256, 333202640600, 4252023300096, 44656994071935, 401490886656000, 3176440229784420, 22567393309593600, 146211911499519294, 874313719685775360, 4872010111798142520, 25497827389410525184, 126142916465781843075, 593121772421445058560, 2662842413150775245160, 11459912788444786513920, 47438786801234168813250, 189449976248893390028800, 731811377318137519245696, 2740630712513624654929920, 9971041659937182693533820, 35307453186561427099877376, 121883284330422510433351500, 410789960190307909157638144, 1353563541518646878675077500, 4365689224858876634610401280, 13798375834642999925542288376, 42780782244213262567058227200, 130233693825770295128044873221, 389608006170995911894300098560, 1146329398900810637779611090240, 3319627709139267167263679606784, 9468166135702260431646263438600, 26614365825753796268872151875584, 73773169969725069760801792854360, 201768789947228738648580043776000, 544763881751616630123165410477688, 1452689254439362169794355429376000, 3827767751739363485065598331130120, 9970416600217443268739409968824320, 25683334706395406994774011866319670, 65452367731499268312170283695144960, 165078821568186174782496283155142200, 412189630805216773489544457234333696, 1019253515891576791938652011091437835, 2496774105950716692603315123199672320, 6060574415413720999542378222812650932, 14581598453215019997540391326153984000, 34782974253512490652111111930326416268, 82282309236048637946346570669250805760, 193075525467822574167329529658775261720, 449497224123337477155078537760754122752, 1038483010587949794068925153685932435825, 2381407585309922413499951812839633584128, 5421449889876564723000378957979772088000, 12255365475040820661535516233050165760000, 27513411092859486460692553086168714659374, 61354289505303613617069338272284858777600, 135925092428365503809701809166616289474168, 299210983800076883665074958854523331870720, 654553043491650303064385476041569995365270, 1423197635972716062310802114654243653681152, 3076095473477196763039615540128479523917200, 6610091773782871627445909215080641586954240, 14123583372861184908287080245891873213544410, 30010041497911129625894110839466234009518080, 63419842535335416307760114920603619461313664, 133312625293210235328551896736236879235481600, 278775024890624328476718493296348769305198947, 579989466306862709777897124287027028934656000, 1200647685924154079965706763561795395948173320, 2473342981183106509136265613239678864092991488, 5070711930898997080570078906280842196519646750, 10346906640850426356226316839259822574115946496, 21015945810275143250691058902482079910086459520, 42493520024686459968969327541404178941239869440, 85539981818424975894053769448098796349808643878, 171444843023856632323050507966626554304633241600, 342155525555189176731983869123583942011978493364, 679986843667214052171954098018582522609944965120, 1345823847068981684952596216882155845897900827370, 2652886321384703560252232129659440092172381585408, 5208621342520253933693153488396012720448385783600, 10186635497140956830216811207229975611480797601792, 19845946857715387241695878080425504863628738882125, 38518943830283497365369391336243138882250145792000, 74484518929289017811719989832768142076931259410120, 143507172467283453885515222342782991192353207603200, 275501042616789153749080617893836796951133929783496, 527036058053281764188089220041629201191975505756160, 1004730453440939042843898965365412981690307145827840, 1908864098321310302488604739098618405938938477379584, 3614432179304462681879676809120464684975130836205250, 6821306832689380776546629825653465084003418476904448, 12831568450930566237049157191017104861217433634289960, 24060143444937604997591586090380473418086401696839680, 44972195698011806740150818275177754986409472910549646, 83798831110707476912751950384757452703801918339072000]

This information will come in handy when we will organize our Monstrous Easter Egg Race, starting tomorrow at 6 am (GMT)…

Leave a Comment

Farey symbols of sporadic groups

Published March 20, 2008 by lievenlb

John Conway once wrote :

There are almost as many different constructions of $M_{24} $ as there have been mathematicians interested in that most remarkable of all finite groups.

In the inguanodon post Ive added yet another construction of the Mathieu groups $M_{12} $ and $M_{24} $ starting from (half of) the Farey sequences and the associated cuboid tree diagram obtained by demanding that all edges are odd. In this way the Mathieu groups turned out to be part of a (conjecturally) infinite sequence of simple groups, starting as follows :

$L_2(7),M_{12},A_{16},M_{24},A_{28},A_{40},A_{48},A_{60},A_{68},A_{88},A_{96},A_{120},A_{132},A_{148},A_{164},A_{196},\ldots $

It is quite easy to show that none of the other sporadics will appear in this sequence via their known permutation representations. Still, several of the sporadic simple groups are generated by an element of order two and one of order three, so they are determined by a finite dimensional permutation representation of the modular group $PSL_2(\mathbb{Z}) $ and hence are hiding in a special polygonal region of the Dedekind’s tessellation

Let us try to figure out where the sporadic with the next simplest permutation representation is hiding : the second Janko group $J_2 $, via its 100-dimensional permutation representation. The Atlas tells us that the order two and three generators act as

e:= (1,84)(2,20)(3,48)(4,56)(5,82)(6,67)(7,55)(8,41)(9,35)(10,40)(11,78)(12, 100)(13,49)(14,37)(15,94)(16,76)(17,19)(18,44)(21,34)(22,85)(23,92)(24, 57)(25,75)(26,28)(27,64)(29,90)(30,97)(31,38)(32,68)(33,69)(36,53)(39,61) (42,73)(43,91)(45,86)(46,81)(47,89)(50,93)(51,96)(52,72)(54,74)(58,99) (59,95)(60,63)(62,83)(65,70)(66,88)(71,87)(77,98)(79,80);

v:= (1,80,22)(2,9,11)(3,53,87)(4,23,78)(5,51,18)(6,37,24)(8,27,60)(10,62,47) (12,65,31)(13,64,19)(14,61,52)(15,98,25)(16,73,32)(17,39,33)(20,97,58) (21,96,67)(26,93,99)(28,57,35)(29,71,55)(30,69,45)(34,86,82)(38,59,94) (40,43,91)(42,68,44)(46,85,89)(48,76,90)(49,92,77)(50,66,88)(54,95,56) (63,74,72)(70,81,75)(79,100,83);

But as the kfarey.sage package written by Chris Kurth calculates the Farey symbol using the L-R generators, we use GAP to find those

L = e*v^-1  and  R=e*v^-2 so

L=(1,84,22,46,70,12,79)(2,58,93,88,50,26,35)(3,90,55,7,71,53,36)(4,95,38,65,75,98,92)(5,86,69,39,14,6,96)(8,41,60,72,61,17, 64)(9,57,37,52,74,56,78)(10,91,40,47,85,80,83)(11,23,49,19,33,30,20)(13,77,15,59,54,63,27)(16,48,87,29,76,32,42)(18,68, 73,44,51,21,82)(24,28,99,97,45,34,67)(25,81,89,62,100,31,94)

R=(1,84,80,100,65,81,85)(2,97,69,17,13,92,78)(3,76,73,68,16,90,71)(4,54,72,14,24,35,11)(5,34,96,18,42,32,44)(6,21,86,30,58, 26,57)(7,29,48,53,36,87,55)(8,41,27,19,39,52,63)(9,28,93,66,50,99,20)(10,43,40,62,79,22,89)(12,83,47,46,75,15,38)(23,77, 25,70,31,59,56)(33,45,82,51,67,37,61)(49,64,60,74,95,94,98)

Defining these permutations in sage and using kfarey, this gives us the Farey-symbol of the associated permutation representation

L=SymmetricGroup(Integer(100))("(1,84,22,46,70,12,79)(2,58,93,88,50,26,35)(3,90,55,7,71,53,36)(4,95,38,65,75,98,92)(5,86,69,39,14,6,96)(8,41,60,72,61,17, 64)(9,57,37,52,74,56,78)(10,91,40,47,85,80,83)(11,23,49,19,33,30,20)(13,77,15,59,54,63,27)(16,48,87,29,76,32,42)(18,68, 73,44,51,21,82)(24,28,99,97,45,34,67)(25,81,89,62,100,31,94)")

R=SymmetricGroup(Integer(100))("(1,84,80,100,65,81,85)(2,97,69,17,13,92,78)(3,76,73,68,16,90,71)(4,54,72,14,24,35,11)(5,34,96,18,42,32,44)(6,21,86,30,58, 26,57)(7,29,48,53,36,87,55)(8,41,27,19,39,52,63)(9,28,93,66,50,99,20)(10,43,40,62,79,22,89)(12,83,47,46,75,15,38)(23,77, 25,70,31,59,56)(33,45,82,51,67,37,61)(49,64,60,74,95,94,98)")

sage: FareySymbol("Perm",[L,R])

[[0, 1, 4, 3, 2, 5, 18, 13, 21, 71, 121, 413, 292, 463, 171, 50, 29, 8, 27, 46, 65, 19, 30, 11, 3, 10, 37, 64, 27, 17, 7, 4, 5], [1, 1, 3, 2, 1, 2, 7, 5, 8, 27, 46, 157, 111, 176, 65, 19, 11, 3, 10, 17, 24, 7, 11, 4, 1, 3, 11, 19, 8, 5, 2, 1, 1], [-3, 1, 4, 4, 2, 3, 6, -3, 7, 13, 14, 15, -3, -3, 15, 14, 11, 8, 8, 10, 12, 12, 10, 9, 5, 5, 9, 11, 13, 7, 6, 3, 2, 1]]

Here, the first string gives the numerators of the cusps, the second the denominators and the third gives the pairing information (where [tex[-2 $ denotes an even edge and $-3 $ an odd edge. Fortunately, kfarey also allows us to draw the special polygonal region determined by a Farey-symbol. So, here it is (without the pairing data) :

the hiding place of $J_2 $…

It would be nice to have (a) other Farey-symbols associated to the second Janko group, hopefully showing a pattern that one can extend into an infinite family as in the inguanodon series and (b) to determine Farey-symbols of more sporadic groups.

Leave a Comment

exotic chess positions (2)

Published March 5, 2008 by lievenlb

Juan de Mairena linked in the comments to last post to a truly great retro-chess problem ! In the position below white is to play and mate in three!



At first this seems wrong as there is an obvious mate in two : 1. Qe2-f1, Kh1xh2 2. Rg3-h3 The ingenious point being that black claims a draw after 1. Qe2-f1 invoking the 50 moves rule which states

The game is drawn, upon a correct claim by the player having the move, if
(a) he writes on his scoresheet, and declares to the arbiter his intention to make a move which shall result in the last 50 moves having been made by each player without the movement of any pawn and without the capture of any piece, or
(b) the last 50 consecutive moves have been made by each player without the movement of any pawn and without the capture of any piece.

I’d love to have the ‘official’ solution to this problem. Here’s what I’ve come up with, spending the better part of the afternoon… It will not be optimal but hopefully isn’t too far off. The crucial part is a maneuver unlocking the lower left-hand cluster of pieces (in particular the ordering of white and black rook). All captures were done with pawns and the final pawn move was b2-b3. Immediately before it the situation might look something like the situation on the left (essential is that the white king should not be too far from its home-square as he will be needed later to block the white rook)



after b2-b3 the bisshop on c1 travels to f4 and the black rook squeezes in to block the white rook so that also the black king can come in and position himself at e2. Then the two rooks evacuate the first row, allowing the black king to go to h1 and then the white king comes in to block the white rook from checking the black king (situation on the left below).



Finally, the white rook comes in and positions itself at e2, afterwards the white king evacuates the first row via b2 and travels to the right-hand upper corner entering via g7. Meanwhile, the black rook comes to g1, the white rook then travels to a3 and the black rook to a2. Then, the white king goes to b7 allowing the bishop to unlock the rook on a8 going to g7, allowing finally the king to go to d8…

Perhaps there is a much simpler and more elegant solution, so if you know, please comment. Oh, btw. how is the original problem solved. Well white first cancels the 50-move rule by 1. Kd8xd7 to continue for example with 2. Rg3-g4, 3. Qe1

10 Comments