Clearly
this cannot be correct for consider for $n \in \mathbb{N} $ the order
$A_n = \begin{bmatrix} \mathbb{C}[x] & \mathbb{C}[x] \\ (x^n) &
\mathbb{C}[x] \end{bmatrix} $
For $m \not= n $ the orders $A_n $
and $A_m $ have isomorphic Azumaya locus, but are not isomorphic as
orders. Still, the statement in the heading is _morally_ what Nikolaus
Vonessen and Zinovy
Reichstein are proving in their paper Polynomial identity
rings as rings of functions. So I better clarify what they do claim
precisely.
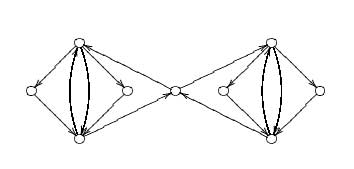
Let $A $ be a _Cayley-Hamilton order_, that is, a
prime affine $\mathbb{C} $-algebra, finite as a module over its center
and satisfying all trace relations holding in $M_n(\mathbb{C}) $. If $A $
is generated by $m $ elements, then its _representation variety_
$\mathbf{rep}_n~A $ has as points the m-tuples of $n \times n $ matrices
$(X_1,\ldots,X_m) \in M_n(\mathbb{C}) \oplus \ldots \oplus
M_n(\mathbb{C}) $
which satisfy all the defining relations of
A. $\mathbf{rep}_n~A $ is an affine variety with a $GL_n $-action
(induced by simultaneous conjugation in m-tuples of matrices) and has
as a Zariski open subset the tuples $(X_1,\ldots,X_m) \in
\mathbf{rep}_n~A $ having the property that they generate the whole
matrix-algebra $M_n(\mathbb{C}) $. This open subset is called the
Azumaya locus of A and denoted by $\mathbf{azu}_n~A $.
One can also define the _generic Azumaya locus_ as being the
Zariski open subset of $M_n(\mathbb{C}) \oplus \ldots \oplus
M_n(\mathbb{C}) $ consisting of those tuples which generate
$M_n(\mathbb{C}) $ and call this subset $\mathbf{Azu}_n $. In fact, one
can show that $\mathbf{Azu}_n $ is the Azumaya locus of a particular
order namely the trace ring of m generic $n \times n $ matrices.
What Nikolaus and Zinovy prove is that for an order A the Azumaya
locus $\mathbf{azu}_n~A $ is an irreducible subvariety of
$\mathbf{Azu}_n $ and that the embedding
$\mathbf{azu}_n~A
\subset \mathbf{Azu}_n $
determines A itself! If you have
worked a bit with orders this result is strange at first until you
recognize it as being essentially a consequence of Bill Schelter's
catenarity result for affine p.i.-algebras.
On the positive
side it shows that the study of orders is roughly equivalent to that of
the study of irreducible $GL_n $-stable subvarieties of $\mathbf{Azu}_n $.
On the negative side, it shows that the $GL_n $-structure of
$\mathbf{Azu}_n $ is horribly complicated. For example, it is still
unknown in general whether the quotient-variety (which is here also the
orbit space) $\mathbf{Azu}_n / GL_n $ is a rational variety.
 Today
Today