If you only tune in now, you might want to have a look at the definition of Mathieu’s blackjack and the first part of the proof of the Conway-Ryba winning strategy involving the Steiner system S(5,6,12) and the Mathieu sporadic group $M_{12} $.
We’re trying to disprove the existence of misfits, that is, of non-hexad positions having a total value of at least 21 such that every move to a hexad would increase the total value. So far, we succeeded in showing that such a misfit must have the patern
$\begin{array}{|c|ccc|} \hline 6 & III & \ast & 9 \\ 5 & II & 7 & . \\ IV & I & 8 & . \\ \hline & & & \end{array} $
That is, a misfit must contain the 0-card (queen) and cannot contain the 10 or 11(jack) and must contain 3 of the four Romans. Now we will see that a misfit also contains precisely one of {5,6} (and consequently also exactly one card from {7,8,9}). To start, it is clear that it cannot contain BOTH 5 and 6 (then its total value can be at most 20). So we have to disprove that a misfit can miss {5,6} entirely (and so the two remaining cards (apart from the zero and the three Romans) must all belong to {7,8,9}).
Lets assume the misfit misses 5 and 6 and does not contain 9. Then, it must contain 4 (otherwise, its column-distribution would be (0,3,3,0) and it would be a hexad). There are just three such positions possible
$\begin{array}{|c|ccc|} \hline . & \ast & \ast & . \\ . & \ast & \ast & . \\ \ast & . & \ast & . \\ \hline – & – & ? & ? \end{array} $ $\begin{array}{|c|ccc|} \hline . & \ast & \ast & . \\ . & . & \ast & . \\ \ast & \ast & \ast & . \\ \hline – & + & ? & ? \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & . \\ . & \ast & \ast & . \\ \ast & \ast & \ast & . \\ \hline – & 0 & ? & ? \end{array} $
Neither of these can be misfits though. In the first one, there is an 8->5 move to a hexad of smaller total value (in the second a 7->5 move and in the third a 7->6 move). Right, so the 9 card must belong to a misfit. Assume it does not contain the 4-card, then part of the misfit looks like (with either a 7- or an 8-card added)
$\begin{array}{|c|ccc|} \hline . & \ast & \ast & \ast \\ . & \ast & ? & . \\ . & \ast & ? & . \\ \hline & & & \end{array} $ contained in the unique hexad $\begin{array}{|c|ccc|} \hline \ast & \ast & \ast & \ast \\ . & \ast & & . \\ . & \ast & & . \\ \hline & & & \end{array} $
Either way the moves 7->6 or 8->6 decrease the total value, so it cannot be a misfit. Therefore, a misfit must contain both the 4- and 9-card. So it is of the form on the left below
$\begin{array}{|c|ccc|} \hline . & ? & \ast & \ast \\ . & ? & ? & . \\ \ast & ? & ? & . \\ \hline & & & \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & . \\ . & \ast & \ast & \ast \\ \ast & \ast & . & . \\ \hline – & 0 & – & + \end{array} $ $\begin{array}{|c|ccc|} \hline . & . & \ast & \ast \\ . & \ast & \ast & . \\ \ast & \ast & . & . \\ \hline & & & \end{array} $
If this is a genuine misfit only the move 9->10 to a hexad is possible (the move 9->11 is not possible as all BUT ONE of {0,1,2,3,4} is contained in the misfit). Now, the only hexad containing 0,4,10 and 2 from {1,2,3} is in the middle, giving us what the misfit must look like before the move, on the right. Finally, this cannot be a misfit as the move 7->5 decreases the total value.
That is, we have proved the claim that a misfit must contain one of {5,6} and one of {7,8,9}. Right, now we can deliver the elegant finishing line of the Kahane-Ryba proof. A misfit must contain 0 and three among {1,2,3,4} (let us call the missing card s), one of $5+\epsilon $ with $0 \leq \epsilon \leq 1 $ and one of $7+\delta $ with $0 \leq \delta \leq 2 $. Then, the total value of the misfit is
$~(0+1+2+3+4-s)+(5+\epsilon)+(7+\delta)=21+(1+\delta+\epsilon-s) $
So, if this value is strictly greater than 21 (and we will see in a moment is has to be if it is at least 21) then we deduce that $s < 1 + \delta + \epsilon \leq 4 $. Therefore $1+\delta+\epsilon $ belongs to the misfit. But then the move $1+\delta \epsilon \rightarrow s $ moves the misfit to a 6-tuple with total value 21 and hence (as we see in a moment) must be a hexad and hence this is a decreasing move! So, finally, there are no misfits!
Hence, from every non-hexad pile of total value at least 21 we have a legal move to a hexad. Because the other player cannot move from an hexad to another hexad we are done with our strategy provided we can show (a) that the total value of any hexad is at least 21 and (b) that ALL 6-piles of total value 21 are hexads. As there are only 132 hexads it is easy enough to have their sum-distribution. Here it is
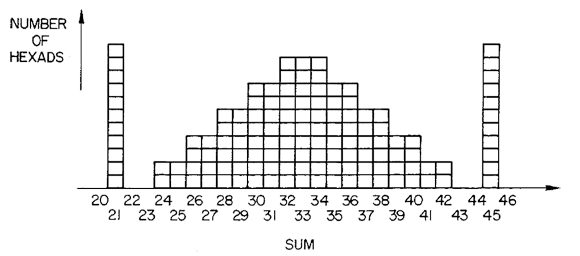
That is, (a) is proved by inspection and we see that there are 11 hexads of sum 21 (the light hexads in Conway-speak) and there are only 11 ways to get 21 as a sum of 6 distinct numbers from {0,1,..,11} so (b) follows. Btw. the obvious symmetry of the sum-distribution is another consequence of the duality t->11-t discussed briefly at the end of part 2.
Clearly, I’d rather have conceptual proofs for all these facts and briefly tried my hand. Luckily I did spot the following phrase on page 326 of Conway-Sloane (discussing the above distribution) :
“It will not be easy to explain all the above observations. They are certainly connected with hyperbolic geometry and with the ‘hole’ structure of the Leech lattice.”
So, I’d better leave it at this…
References
Joseph Kahane and Alexander J. Ryba, “The hexad game“
John H. Conway and N. J.A. Sloane, “Sphere packings, Lattices and Groups” chp. 11 ‘The Golay codes and the Mathieu groups’
 Ernst Witt knew already that there are just two even unimodular lattices in 16 dimensions : $E_* \oplus E_8 $ and $D_{16}^+ $ and as there is just one modular form of weigth 8 upto scalars, the theta function cannot determine the latice in 16 dimensions. The number of dimensions for a counterexamle was sunsequently reduced to 12 (Kneser), 8 (Kitaoka),6 (Sloane) and finally 4 (Schiemann).
Ernst Witt knew already that there are just two even unimodular lattices in 16 dimensions : $E_* \oplus E_8 $ and $D_{16}^+ $ and as there is just one modular form of weigth 8 upto scalars, the theta function cannot determine the latice in 16 dimensions. The number of dimensions for a counterexamle was sunsequently reduced to 12 (Kneser), 8 (Kitaoka),6 (Sloane) and finally 4 (Schiemann).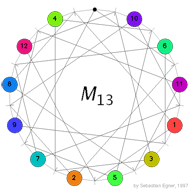 Conway’s puzzle M(13) involves the 13 points and 13 lines of $\mathbb{P}^2(\mathbb{F}_3) $. On all but one point numbered counters are placed holding the numbers 1,…,12 and a move involves interchanging one counter and the ‘hole’ (the unique point having no counter) and interchanging the counters on the two other points of the line determined by the first two points. In the picture on the left, the lines are respresented by dashes around the circle in between two counters and the points lying on this line are those that connect to the dash either via a direct line or directly via the circle. In the
Conway’s puzzle M(13) involves the 13 points and 13 lines of $\mathbb{P}^2(\mathbb{F}_3) $. On all but one point numbered counters are placed holding the numbers 1,…,12 and a move involves interchanging one counter and the ‘hole’ (the unique point having no counter) and interchanging the counters on the two other points of the line determined by the first two points. In the picture on the left, the lines are respresented by dashes around the circle in between two counters and the points lying on this line are those that connect to the dash either via a direct line or directly via the circle. In the 