Yesterday, Ed Segal gave a talk at the Arts. His title “Superpotential algebras from 3-fold singularities” didnt look too promising to me. And sure enough it was all there again : stringtheory, D-branes, Calabi-Yaus, superpotentials, all the pseudo-physics babble that spreads virally among the youngest generation of algebraists and geometers.
Fortunately, his talk did contain a general ringtheoretic gem. After a bit of polishing up this gem, contained in his paper The A-infinity Deformation Theory of a Point and the Derived Categories of Local Calabi-Yaus, can be stated as follows.
Let $A $ be a $\mathbb{C} $-algebra and let $M = S_1 \oplus \ldots \oplus S_k $ be a finite dimensional semi-simple representation with distinct simple components. Let $\mathfrak{m} $ be the kernel of the algebra epimorphism $A \rightarrow S $ to the semi-simple algebra $S=End(M) $. Then, the $\mathfrak{m} $-adic completion of $A $ is Morita-equivalent to the completion of a quiver-algebra with relations. The nice thing is that both the quiver and relations come in a canonical way from the $A_{\infty} $-structure on the Ext-algebra $Ext^{\bullet}_A(M,M) $. More precisely, there is an isomorphism
$\hat{A}_{\mathfrak{m}} \simeq \frac{\hat{T}_S(Ext^1_A(M,M)^{\ast})}{(Im(HMC)^{\ast})} $
where the homotopy Maurer-Cartan map comes from the $A_{\infty} $ structure maps
$HMC = \oplus_i m_i~:~T_S(Ext_A^1(M,M)) \rightarrow Ext^2_A(M,M) $
and hence the defining relations of the completion are given by the image of the dual of this map.
For ages, Ive known this result in the trivial case of formally smooth algebras (where $Ext^2_A(M,M)=0 $ and hence there are no relations to divide out) and where it is a consequence of a special case of the Cuntz-Quillen “tubular neighborhood” result. Completions of formally smooth algebras at semi-simples are Morita equivalent to completions of path algebras. This fact motivated all the local-quiver technology that was developed here in Antwerp over the last decade (see my book if you want to know the details).
Also for 3-dimensional Calabi-Yau algebras it states that the completions at semi-simples are Morita equivalent to completions of quotients of path algebras by the relations coming from a superpotential (aka a necklace) by taking partial noncommutative derivatives. Here the essential ingredient is that $Ext^2_A(M,M)^{\ast} \simeq Ext^1_A(M,M) $ in this case.
One Comment
Farey sequences have plenty of mysterious properties. For example, in 1924 J. Franel and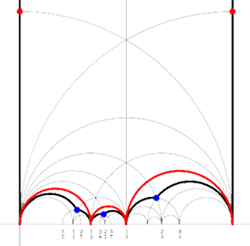 
Recall from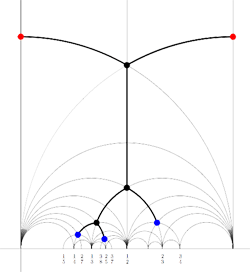 
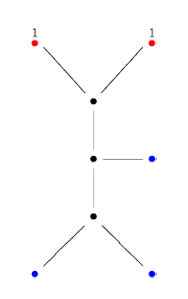
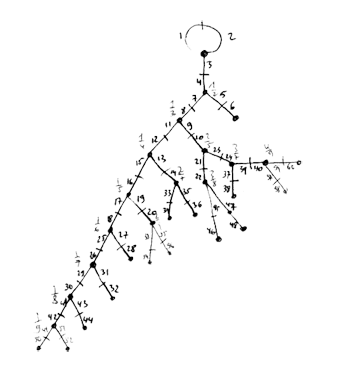
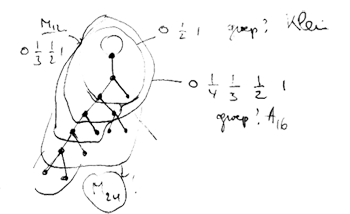
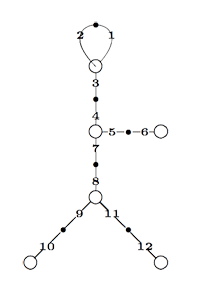Finally, identifying the red points (as they lie on geodesics connected to $\infty $ which are identified in the Farey code), adding even points on the remaining geodesics and numbering the obtained half-lines we obtain the dessin d’enfant given on the left hand side. To such a dessin we can associate its monodromy group which is a permutation group on the half-lines generated by an order two element indicating which half-lines make up a line and an order three element indicating which half-lines one encounters by walking counter-clockwise around a three-valent vertex. For the dessin on the left the group is therefore the subgroup of $S_{12} $ generated by the elements
