 Via the Arcadian functor I learned of the existence of the Sudokube (picture on the left).
Via the Arcadian functor I learned of the existence of the Sudokube (picture on the left).
Sudokube is a variation on a Rubik’s Cube in which each face resembles one-ninth of a Sudoku grid: the numbers from one to nine. This makes solving the cube slightly more difficult than a conventional Rubik’s Cube because each number must be in the right place and the centre cubies must also be in the correct orientation.
A much more interesting Sudoku-variation of the cube was invented two weeks ago by one of my freshmen-grouptheory students and was dubbed the mini-sudokube by him. Here’s the story.
At the end of my grouptheory course I let the students write a paper to check whether they have research potential. This year the assignment was to read through the paper mini-sudokus and groups by Carlos Arcos, Gary Brookfield and Mike Krebs, and do something original with it.
Mini-Sudoku is the baby $2 \times 2 $ version of Sudoku. Below a trivial problem and its solution
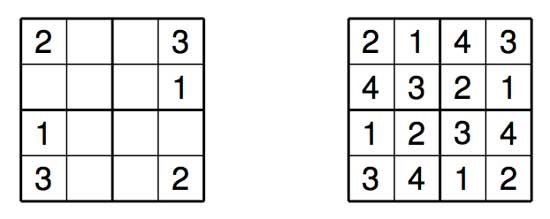
Of course most of them took the safe road and explained in more detail a result of the paper. Two of them were more original. One used the mini-sudoku solutions to find solutions for 4×4 sudokus, but the most original contribution came from Ibrahim Belkadi who wanted to count all mini-sudokubes. A mini-sudokube is a cube with a mini-sudoku solution on all 6 of its sides BUT NUMBERS CARRY OVER CUBE-EDGES. That is, if we have as the mini-sudoku given by the central square below on the top-face of the cube, then on the 4 side-faces we have already one row filled in.
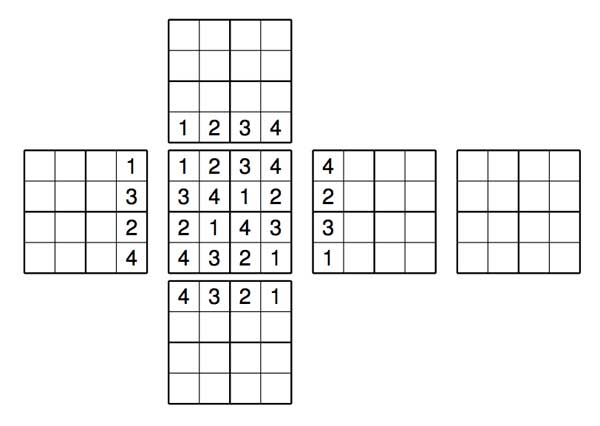
The problem then is to find out how many compatible solutions there are. It is pretty easy to see that top- and bottom-faces determine all squares of the cube, but clearly not all choices are permitted. For example, with the above top-face fixed there are exactly 4 solutions. Let ${ a,b } = { 1,4 } $ and ${ c,d } = { 2,3 } $ then these four solutions are given below
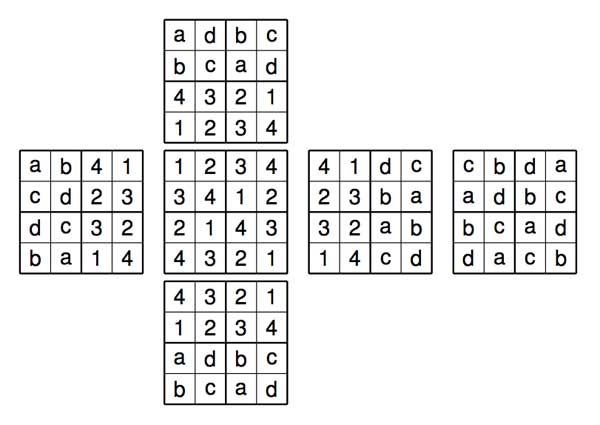
Putting one of these solutions (or any other) on a $4 \times 4 $-Rubik cube would make a more interesting puzzle, I think. I’ve excused Ibrahim from having to take examination on condition that he writes down what he can prove on his mini-sudokubes by that time. Looking forward to it!
One Comment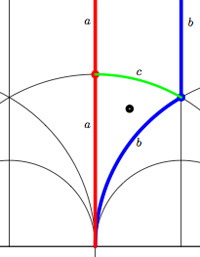 For example, the modular group itself is represented by the Farey symbol
For example, the modular group itself is represented by the Farey symbol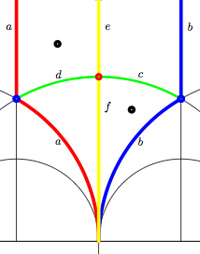 Okay, let’s look at the next case, that of the unique index 2 subgroup $\Gamma_2 $ represented by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{\bullet} & 0 \ar@{-}[r]_{\bullet} & \infty}[/tex] or the dessin (the two green edges) or by its fundamental domain consisting of the 4 triangles where again the left and right vertical boundaries are to be identified in parts.
Okay, let’s look at the next case, that of the unique index 2 subgroup $\Gamma_2 $ represented by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{\bullet} & 0 \ar@{-}[r]_{\bullet} & \infty}[/tex] or the dessin (the two green edges) or by its fundamental domain consisting of the 4 triangles where again the left and right vertical boundaries are to be identified in parts.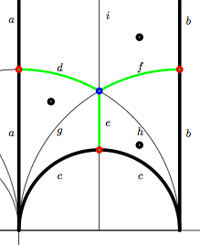 As a mental check, verify that the index 3 subgroup determined by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{\circ} & 1 \ar@{-}[r]_{\circ} & \infty}[/tex] , whose fundamental domain with identifications is given on the left, has as its associated quiver picture
As a mental check, verify that the index 3 subgroup determined by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{\circ} & 1 \ar@{-}[r]_{\circ} & \infty}[/tex] , whose fundamental domain with identifications is given on the left, has as its associated quiver picture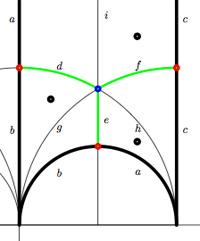 whereas the index 3 subgroup determined by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{1} & 0 \ar@{-}[r]_{1} & 1 \ar@{-}[r]_{\circ} & \infty}[/tex], whose fundamental domain with identifications is depicted on the right, has as its associated quiver
whereas the index 3 subgroup determined by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{1} & 0 \ar@{-}[r]_{1} & 1 \ar@{-}[r]_{\circ} & \infty}[/tex], whose fundamental domain with identifications is depicted on the right, has as its associated quiver