The main application of tori to cryptography is to exchange keys more efficiently while preserving the same security standards.
In the Diffie-Hellman key-exchange one interchanges elements of the finite field $\mathbb{F}_q $ where $q=p^N $ is a prime-power of a large prime number $p $. If we call an element of the prime field $\mathbb{F}_p $ a pit (similar to bit when $p=2 $) then we can measure transmssions in pits. An element $h \in \mathbb{F}_q $ requires N pits, for we can write the finite field as the quotient of ring of polynomials $\mathbb{F}_p[x] $
$\mathbb{F}_q = \frac{\mathbb{F}_p[x]}{(f(x))} $
modulo an _irreducible_ polynomial $f(x) $ of degree N. Hence, any $h \in \mathbb{F}_q $ can be written as a polynomial of degree $< N $,
$h = a_1 + a_2 x + \ldots + a_N x^{N-1} $
with all $a_i \in \mathbb{F}_p $, so we can represent $h=(a_1,a_2,\ldots,a_N) $ as N pits. Now, we are going to limit this number of pits (from $N $ to about $\phi(N) $ where $\phi $ is the Euler totient function, that is the number of integers smaller than N and coprime to it) by restricting the elements $h $ to be transfered to a subgroup of the group of units of the finite field $\mathbb{F}_q^* $ while not compromising on the security of the public key system (the large order of the basic element $g \in \mathbb{F}_q^* $ of which $h $ is a power).
 To see that this is indeed possible, let us consider the easiest case (that of $N=2 $) and keep the discussion tori-free (those of you who know more will realize that Hilbert’s Satz 90 is never too far away…). If $q=p^2 $ then the order of the cyclic group $\mathbb{F}_q^* $ is $p^2-1 = (p-1)(p+1) $ so in order to get a safe system let us choose the large prime number $p $ such that also tex/2=r $ is a prime number.
To see that this is indeed possible, let us consider the easiest case (that of $N=2 $) and keep the discussion tori-free (those of you who know more will realize that Hilbert’s Satz 90 is never too far away…). If $q=p^2 $ then the order of the cyclic group $\mathbb{F}_q^* $ is $p^2-1 = (p-1)(p+1) $ so in order to get a safe system let us choose the large prime number $p $ such that also tex/2=r $ is a prime number.
Right, now define $T_2 $ to be the subgroup of $\mathbb{F}_q^* $ of order $p+1 $ and let $g $ be a generator of it that we will use in the Diffie-Hellman exchange. Can we describe the element of $T_2 $ (our torus in disguise)? Take $d \in \mathbb{F}_p^* $ a non-square element, then we can write
$\mathbb{F}_q = \mathbb{F}_p(\sqrt{d}) $ and $T_2 = { a+b\sqrt{d}~:~(a+b\sqrt{d})^{p+1}=1 } $ (here, $a,b \in \mathbb{F}_p $). But we claim that
$~(a+b\sqrt{d})^p = a -b \sqrt{d} $. Indeed, $a^p=a,b^p=b $ and from Fermat’s little theorem we deduce that
$ -1 = (\frac{d}{p}) \equiv d^{\frac{p-1}{2}}~mod(p) $
where the middle term is the Legendre symbol which is equal to -1 because d was a non-square modulo p. That is, we can then write $T_2 $ as the algebraic variety of dimension one defined over $\mathbb{F}_p $ and given by the equation
$T_2 = { a+b\sqrt{d} \in \mathbb{F}_q^*~\mid~(a,b) \in \mathbb{F}^2~:~a^2-db^2=1 } $
Because $T_2 $ is of dimension one over $\mathbb{F}_p $ we can hope that most of its elements can be represented by just one pit (instead of the two pits necessary to represent them as elements of $\mathbb{F}_q $). This is indeed the case, for we have explicit maps (in geometric terms, these maps show that $T_2 $ is a rational variety)
$j~:~\mathbb{F}_p \rightarrow T_2~\quad~j(a) = \frac{a+\sqrt{d}}{a-\sqrt{d}}=\frac{a^2+d}{a^2-d}+\frac{2a}{a^2-d}\sqrt{d} $
which has a well-defined invers on the complement of ${ 1,-1 } $
$f~:~T_2 – { 1,-1 } \rightarrow \mathbb{F}_p~\quad~f(a+b\sqrt{d}) = \frac{1+a}{b} $
From the right-hand description of $j(a) $ one deduces that indeed we have that $f(j(a))=a $. Using this we can indeed compress the Diffie-Hellman exchange by a factor 2.
Instead of giving you the element $g^a \in T_2 $ computed using my secret number a, I’ll send you (using only one pit) the number $f(g^a) \in \mathbb{F}_p $. On this number, you can apply the j-function to recover $g^a $ and then compute the common key $~(g^a)^b = g^{ab} $ using your secret number b). Still, we didnt compromise on security because we used the most difficult elements around in $\mathbb{F}_q^* $. By going to higher dimensional tori one can even improve on the efficiency rate!
3 Comments Whitfield Diffie (r.) and Martin Hellman (m.) published in 1976 their public key-exchange system. Take a large prime power $q=p^N $, make it public and consider the finite field $\mathbb{F}_q $ which is known to have a cyclic group of units $\mathbb{F}^*_q $ of order $q-1 $. Now, take $g $ to be an element in it of large order (preferable a generator but that isnt necessary) and also make this element public.
Whitfield Diffie (r.) and Martin Hellman (m.) published in 1976 their public key-exchange system. Take a large prime power $q=p^N $, make it public and consider the finite field $\mathbb{F}_q $ which is known to have a cyclic group of units $\mathbb{F}^*_q $ of order $q-1 $. Now, take $g $ to be an element in it of large order (preferable a generator but that isnt necessary) and also make this element public. And that was the full story until 1997. In December, 1997, it was revealed that researchers at the
And that was the full story until 1997. In December, 1997, it was revealed that researchers at the 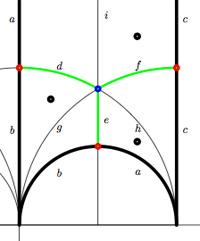 We have
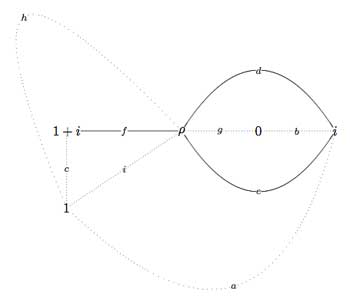
We have  On the left, a quilt-diagram copied from Hsu’s book
On the left, a quilt-diagram copied from Hsu’s book