The
moment I read about it, I ordered the book, but received at least three
emails from Amazon.co.uk apologizing for not being able to find me a
copy of Lee Smolin’s The trouble with physics.
A very
considerate review of the book can be found at Background Independence, Christine Dantas’
old blog. Btw. I’m happy Christine has set up a new blog called
Theorema Egregium. Here’s the section
in her review that convinced me to have a look at the book myself.
I do not wish to make public some of my old, deep own
feelings about what I think science is and how it should be conducted.
There are of course certain points that I often do make public, but
there are some others that tormented me for quite a long time now, and
are so personal and even of emotive nature that I would rather keep them
to myself. But this is the fact per se that should be mentioned here,
since this is the contribution that I feel I can give on examining his
book: I found out that he was addressing some of my personal views and
doubts, of course from his own perspective and wisdom, but it was like
talking to an old friend who followed my own career in science and
understood what troubled me most for all those years. So this book is
for you if you want to be challenged over your own vision of science and
how you fit in it.
Finally, after all these months, just
before going on vacation I discovered a copy in one of my favourite
bookshops in Antwerp and took it along. I dont know Christine’s
favourite chapters of the book but I feel somehow I’ll be not too far
off mark in believing that chapter 16 “How Do You Fight Sociology?” will
be among them. This chapter (just 27 pages) should be read and reread by
all scientists. In it, Lee Smolin describes community behaviour of
certain scientific groups (he has the stringtheory-community in mind but
I’m sure anyone will recognise some of its behavior in groups closer to
ones own research-interests. I certainly did…). Here we go (citing
from page 284)
1. _Tremendous self-confidence_ ,
leading to a sense of entitlement and of belonging to an elite of
experts.
2. _An unusually monolithic community_ , with a
strong sense of consensus, whether driven by evidence or not, and an
unusual uniformity of views on open questions. These views seem related
to the existence of a hierarchical structure in which ideas of a few
leaders dictate the viewpoint, strategy, and direction of the field,
3. In some cases, a _sense of identification with the group_ ,
akin to identification with a religious faith or political platform.
4. A strong sense of the _boundary between the group and other
experts_ .
5. A _disregard for and disinterest in_ the
ideas, opinions, and work of experts who are not part of the group, and
a preference for talking only with other members of the commnity.
6. A tendency to _interpret evidence optimistically_ , to believe
exaggerated or incorrect statements of results, and to disregard the
possibility that the theory might be wrong. This is coupled with a
tendency to _believe results are true because they are widely
believed’_ even if one has not checked (or even seen) the proof
oneself.
7. A lack of appreciation for the extent to which a
research program ought to involve risk.
Although spotting
such behaviour can be depressing and/or frustrating, Smolin’s analysis
is that such groups are doomed to perish sooner or later for it is
exactly the kind of behaviour sociologists and psychologists recognize
as groupthink, following the Yale psychologist Irving Janis, “a mode
of thinking that people engage in when they are deeply involved in a
cohesive in-group, when the members’ strivings for unanimity override
their motivation to realistically appraise alternative courses of
action”. Groupthink is responsable for failures of decision making by
groups of experts such as the “failure of NASA to prevent the Challenger
disaster, the failure of the West to anticipate the collapse of the
Soviet Union, the failure of the American automobile companies to
feresee the demand for smaller cars, and most recently – and perhaps
most calamitously – the Bush administration’s rush to war on the basis
of a false belief that Iraq had weapons of mass destruction.” (Smolin,
page 286). An aspect of these groupthinking science-groups that worries
me most of all is their making of exagerated claims to potential
applications, not supported (yet) by solid proof. Short-time effect may
be to attract more people to the subject and to keep doubting followers
on board, but in the long term (at least if the claimed results remain
out of reach) this will destroy the subject itself (and, sadly enough,
also closeby subjects making no outrageous claims…). My advice to
people making such claims is : do a Perelman! Rather than doing a
PR-job, devote yourself for as long as it takes to prove your hopes,
somewhere in splendid isolation and come back victoriously. I have a
spare set of keys if you are in search for the perfect location…


 and related it to
and related it to But from this
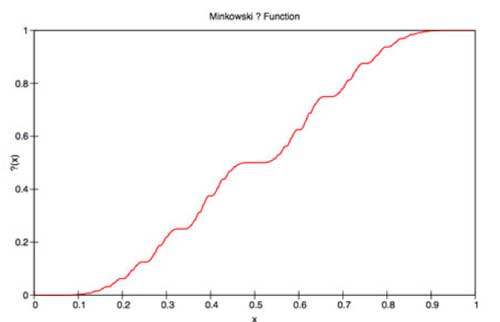
But from this That is, $?(x-1) = 1 – ?(x) $ Observe that the left-hand
That is, $?(x-1) = 1 – ?(x) $ Observe that the left-hand